【2018一橋大学】
\(a\) を実数とし,\(f(x)=x-x^3\) , \(g(x)=a(x-x^2)\) とする.\(2\) つの曲線 \(y=f(x)\) , \(y=g(x)\) は \(0<x<1\) の範囲に共有点を持つ.
(1) \(a\) のとりうる値の範囲を求めよ.
(2) \(y=f(x)\) と \(y=g(x)\) で囲まれた \(2\) つの部分の面積が等しくなるような \(a\) の値を求めよ.
\(2\) 曲線で囲まれた \(2\) つの部分の面積が等しい条件
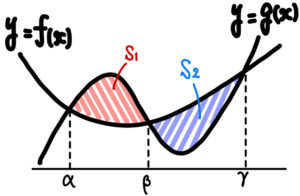
\(y=f(x)\) と \(y=g(x)\) が \(x=\alpha,\beta,\gamma\)
( \(\alpha<\beta<\gamma\) ) の共有点をもち,
\(2\) 曲線 \(y=f(x)\) と \(y=g(x)\) で囲まれた \(2\) つの部分の面積が等しいとき
\(\displaystyle\int^{\gamma}_{\alpha} \left\{g(x)-f(x)\right\} dx=0\)
\(S_{1}=\displaystyle\int^{\beta}_{\alpha} \left\{g(x)-f(x)\right\} dx\)
\(S_{2}=\displaystyle\int^{\gamma}_{\beta} \left\{f(x)-g(x)\right\} dx\)
より,\(S_{1}=S_{2}\) \(\iff\) \(S_{1}-S_{2}=0\) のとき
\(\displaystyle\int^{\beta}_{\alpha} \left\{g(x)-f(x)\right\} dx-\displaystyle\int^{\gamma}_{\beta} \left\{f(x)-g(x)\right\} dx=0\)
\(\iff\) \(\displaystyle\int^{\beta}_{\alpha} \left\{g(x)-f(x)\right\} dx+\displaystyle\int^{\gamma}_{\beta} \left\{g(x)-f(x)\right\} dx=0\)
よって,\(\displaystyle\int^{\gamma}_{\alpha} \left\{g(x)-f(x)\right\} dx=0\)
解答
(1)
\(f(x)=g(x)\) より
\(x-x^3=a(x-x^2)\)
\(x(x-1)(x-a+1)=0\)
\(x=0,1,a-1\)
条件より
\(0<a-1<1\)
よって,\(1<a<2\)
(2)
\(y=f(x)\) と \(y=g(x)\) で囲まれた \(2\) つの部分の面積が等しくなるとき
\(\displaystyle\int^{1}_{0} \left\{g(x)-f(x)\right\}dx=0\) が成り立つ.
よって,\(\displaystyle\int^{1}_{0} (x^3-ax^2+ax-x) dx=0\)
\(\Bigl[\displaystyle\frac{1}{4}x^4-\displaystyle\frac{a}{3}x^3+\displaystyle\frac{a-1}{2}x^2\Bigr]^{1}_{0}=0\)
\(a=\displaystyle\frac{3}{2}\) ( これは \(1<a<2\) を満たす )







コメント