【2023藤田医科大学(後期)医学部・第２問】
\(O\) を原点とする \(xy\) 平面上に点 \(A(2,0)\) ，点 \(B(1,\sqrt{3})\) ，および実数 \(s\) ，\(t\) と \(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\) により定まる点 \(P\) がある． \(s\) ，\(t\) が(１)〜(３)のそれぞれの条件を満たす場合について，点 \(P\) がとりうる範囲を \(xy\) 平面上に図示し，その面積を求めよ．
(１) \(2≦s+2t≦6\)，\(0≦s\)，\(0≦t\)
(２) \(1≦|s|+|t|≦6\)
(３) \(s^2+(s+t)^2≦6\)
平面上の点の存在(異なる \(2\) 点を通る直線のベクトル方程式)
異なる \(2\) 点 \(A(\overrightarrow{a})\)，\(B(\overrightarrow{b})\) を通る直線のベクトル方程式は
・\(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\) かつ \(s+t=1\)
さらに，\(s≧0\)，\(t≧0\) のとき点 \(P\) の存在範囲は，『 線分 \(AB\) 』 となる．
\(\triangle OAB\) に対して，点 \(P\) が
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\)，\(0≦s+t≦1\)，\(s≧0\)，\(t≧0\)
を満たしながら動くとき，点 \(P\) の存在範囲は『 \(\triangle OAB\) の周および内部 』となる．
解答・解説
(１) \(2≦s+2t≦6\)，\(0≦s\)，\(0≦t\)
\(s+2t=2\)，\(0≦s\)，\(0≦t\) ・・・① のとき
\(\displaystyle\frac{1}{2}s+t=1\) より
\(\overrightarrow{OP}=\displaystyle\frac{1}{2}s\left(2\overrightarrow{OA}\right)+t\overrightarrow{OB}\)
よって①を満たす点 \(P\) の存在範囲は
\(2\overrightarrow{OA}=(4,0)\) と \(\overrightarrow{OB}=(1,\sqrt{3})\) の終点を結ぶ線分となる．
\(s+2t=6\)，\(0≦s\)，\(0≦t\) ・・・② のとき
\(\displaystyle\frac{1}{6}s+\displaystyle\frac{1}{3}t=1\) より
\(\overrightarrow{OP}=\displaystyle\frac{1}{6}s\left(6\overrightarrow{OA}\right)+\displaystyle\frac{1}{3}t\left(3\overrightarrow{OB}\right)\)
よって②を満たす点 \(P\) の存在範囲は
\(6\overrightarrow{OA}=(12,0)\) と \(3\overrightarrow{OB}=(3,3\sqrt{3})\) の終点を結ぶ線分となる．
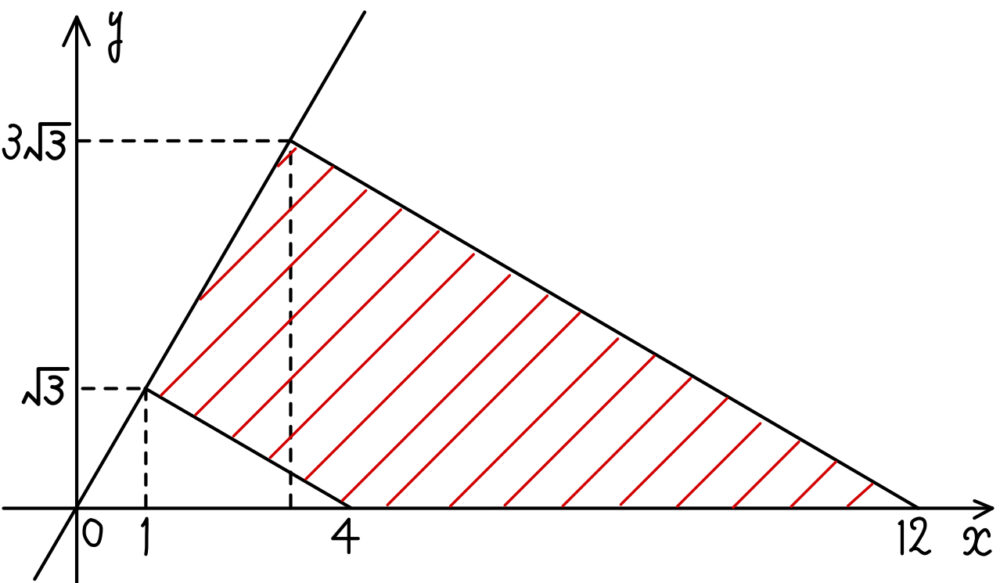よって，\(2≦s+2t≦6\)，\(0≦s\)，\(0≦t\) を満たす点 \(P\) の存在範囲は右図の斜線部分の四角形の周および内部
したがって求める面積は
\(\displaystyle\frac{1}{2}\cdot 12\cdot 3\sqrt{3}-\displaystyle\frac{1}{2}\cdot 4\cdot \sqrt{3}=16\sqrt{3}\)
(２) \(1≦|s|+|t|≦6\)
( ⅰ ) \(s≧0\) ，\(t≧0\) のとき
\(1≦s+t≦6\) を満たす領域は(１)と同様に考えると
\(4\) 点 \((2,0)\) ，\((12,0)\) ，\((6,6\sqrt{3})\) ，\((1,\sqrt{3})\) でできる四角形の周および内部．
この部分の面積は，\(\displaystyle\frac{1}{2}\cdot 12\cdot 6\sqrt{3}-\displaystyle\frac{1}{2}\cdot 2\cdot \sqrt{3}=35\sqrt{3}\)
( ⅱ ) \(s≧0\) ，\(t≦0\) のとき
\(1≦s-t≦6\) \(\iff\) \(1≦s+(-t)≦6\) であり
\(\overrightarrow{OP}=s\overrightarrow{OA}+(-t)\left(-\overrightarrow{OB}\right)\) として考えると
これを満たす領域は
\(4\) 点 \((2,0)\) ，\((12,0)\) ，\((-6,-6\sqrt{3})\) ，\((-1,-\sqrt{3})\) でできる四角形の周および内部．
この部分の面積は，\(\displaystyle\frac{1}{2}\cdot 12\cdot 6\sqrt{3}-\displaystyle\frac{1}{2}\cdot 2\cdot \sqrt{3}=35\sqrt{3}\)
\(x≦0,y≧0\) のとき，\(x≦0,y≦0\) のときについても( ⅰ )( ⅱ )と対称な図形が得られるので，求める面積はいずれも \(35\sqrt{3}\)
したがって求める図形の面積は，\(35\sqrt{3}\times 4=140\sqrt{3}\)
(３) \(s^2+(s+t)^2≦6\)
\(P(x,y)\) とおくと，\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\) より
\(\overrightarrow{OP}=(2s+t,\sqrt{3}t)\) なので
\(\begin{cases}x=2s+t\\y=\sqrt{3}t\end{cases}\) \(\iff\) \(\begin{cases}s=\displaystyle\frac{1}{2\sqrt{3}}(\sqrt{3}x-y)\\t=\displaystyle\frac{1}{\sqrt{3}}y\end{cases}\)
\(s^2+(s+t)^2≦6\) に代入すると
\(\displaystyle\frac{(\sqrt{3}x-y)^2}{12}+\displaystyle\frac{(\sqrt{3}x+y)^2}{12}≦6\)
よって，\(\displaystyle\frac{x^2}{12}+\displaystyle\frac{y^2}{36}≦1\)
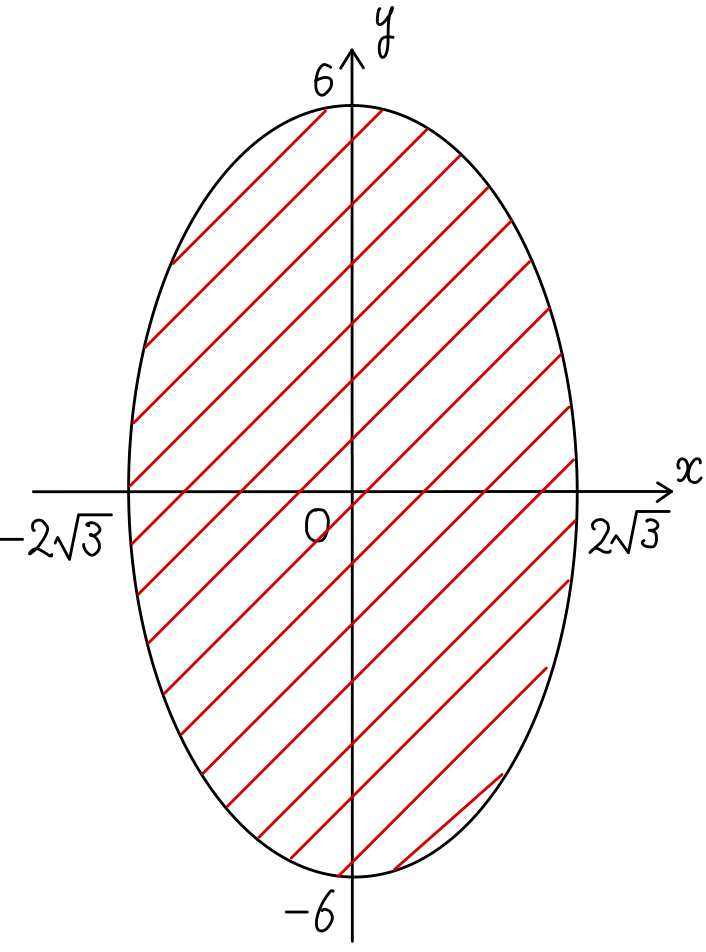
したがって求める図形は，右図の楕円の周および内部であるので
その面積は \(\pi\cdot 2\sqrt{3}\cdot 6=12\sqrt{3}\pi\)
楕円の面積公式
コメント