【2023北海道大学・理系・第3問】
以下の問いに答えよ.ただし,\(e\) は自然対数の底を表す.
(1) \(k\) を実数の定数とし,\(f(x)=xe^{-x}\) とおく.方程式 \(f(x)=k\) の異なる実数解の個数を求めよ.ただし,\(\displaystyle\lim_{x\rightarrow\infty}f(x)=0\) を用いてもよい.
(2) \(xye^{-(x+y)}=c\) をみたす正の実数 \(x\),\(y\) の組がただ \(1\) つ存在するときの実数 \(c\) の値を求めよ.
(3) \(xye^{-(x+y)}=\displaystyle\frac{3}{e^4}\) をみたす正の実数 \(x\),\(y\) を考えるとき,\(y\) のとりうる値の最大値とそのときの \(x\) の値を求めよ.
解答・解説
(1)
\(f(x)=xe^{-x}\) のとき
\(f^{\prime}(x)=(1-x)e^{-x}\) より
| \(x\) | ・・・ | \(1\) | ・・・ |
| \(f^{\prime}(x)\) | + | \(0\) | ー |
| \(f(x)\) | ↗️ | \(\displaystyle\frac{1}{e}\) | ↘️ |
\(\displaystyle\lim_{x\rightarrow -\infty}f(x)=-\infty\) ,\(\displaystyle\lim_{x\rightarrow\infty}f(x)=0\) より
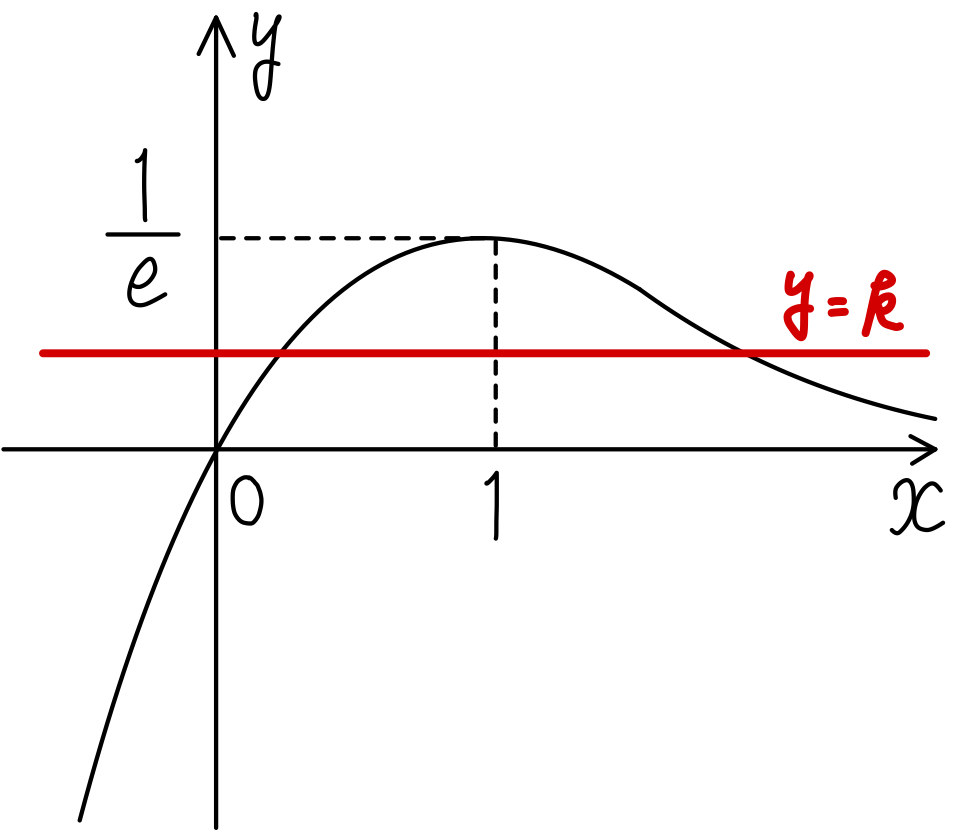 右図のグラフから,求める異なる実数解の個数は
右図のグラフから,求める異なる実数解の個数は
\(k≦0\) のとき \(1\) 個
\(0<k<\displaystyle\frac{1}{e}\) のとき \(2\) 個
\(k=\displaystyle\frac{1}{e}\) のとき \(1\) 個
\(k>\displaystyle\frac{1}{e}\) のとき \(0\) 個
(2)
\(xye^{-(x+y)}=c\) より
\(xe^{-x}ye^{-y}=c\)
(1)のグラフから \(x>0\),\(y>0\) のとき
\(0<xe^{-x}≦\displaystyle\frac{1}{e}\),\(0<ye^{-y}≦\displaystyle\frac{1}{e}\)
よって \(0<xe^{-x}ye^{-y}≦\displaystyle\frac{1}{e^2}\)
等号成立は \(xe^{-x}=\displaystyle\frac{1}{e}\) かつ \(ye^{-y}=\displaystyle\frac{1}{e}\)
よって \((x,y)=(1,1)\)
ゆえに,\(c=\displaystyle\frac{1}{e^2}\) のとき,与式をみたす正の実数 \(x\),\(y\) の組は \((1,1)\) の \(1\) 組となる.
また,(1)より \(0<xe^{-x}<\displaystyle\frac{1}{e}\) をみたす値を \(1\) つ定めるとき,それに対応する正の実数 \(x\) の値は異なる \(2\) つ存在し,\(y\) についても同様.
よって \(0<xe^{-x}ye^{-y}<\displaystyle\frac{1}{e^2}\) をみたす値を \(1\) つ定めると,それに対応する正の実数 \(x\),\(y\) の組は複数存在する.
さらに \(xe^{-x}<0,\displaystyle\frac{1}{e^2}<xe^{-x}\) をみたす値を \(1\) つ定めるとき,それに対応する正の実数 \(x\) は存在せず,\(y\) についても同様.
よって \(xe^{-x}ye^{-y}<0,\displaystyle\frac{1}{e^2}<xe^{-x}ye^{-y}\) をみたす値を \(1\) つ定めると,それに対応する正の実数 \(x\),\(y\) の組は存在しない.
したがって,題意をみたす \(c=\displaystyle\frac{1}{e^2}\)
(3)
\(x>0\),\(y>0\) のとき
\(xye^{-(x+y)}=\displaystyle\frac{3}{e^4}\)
\(xe^{-x}=\displaystyle\frac{3}{e^4ye^{-y}}\) ・・・①
\(0<xe^{-x}≦\displaystyle\frac{1}{e}\) より
\(0<\displaystyle\frac{3}{e^4ye^{-y}}≦\displaystyle\frac{1}{e}\)
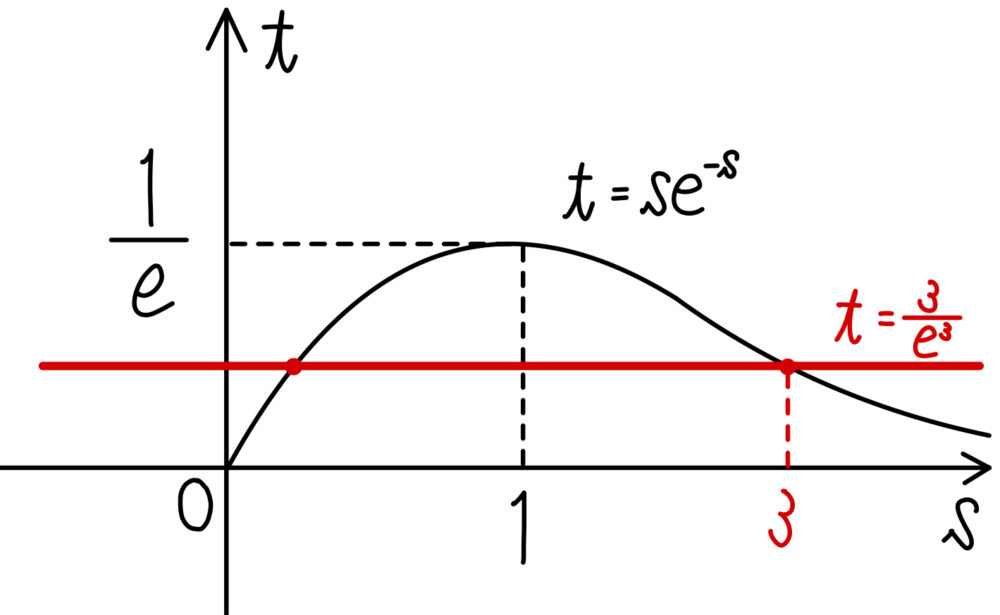 よって \(ye^{-y}≧\displaystyle\frac{3}{e^3}\)
よって \(ye^{-y}≧\displaystyle\frac{3}{e^3}\)
右図から \(y\) のとりうる値の最大値は \(y=3\)
このとき①より \(xe^{-x}=\displaystyle\frac{1}{e}\)
よって \(x=1\)







コメント