【2023久留米大学・医学部】
\(n\) を正の整数とする.連立不等式
\(\begin{cases}y≧2^{\log_{2}{x}+x}\\y≦-x^2+n(2^n+n)\end{cases}\)
で表される領域を \(D_{n}\) とする.ただし,\(x\) 座標と \(y\) 座標がともに整数となる点を「格子点」と呼ぶものとする.
(1) 省略
(2) \(S=1\cdot 2+2\cdot 2^2+3\cdot 2^3+\cdots+n\cdot 2^n\) とするとき,\(S\) を計算せよ.
(3) \(D_{n}\) に含まれる格子点の個数を \(n\) を用いて表せ.
(2)等差×等比数列の総和について
等差数列 \(\times\) 等比数列の総和(Σ)
⇒ 公比をかけて,差をとる.
(3)格子点について
格子点とは
格子点とは,\(x\) 座標も \(y\) 座標も整数である点のこと.

難関大学では頻出の分野の1つです!
有名な問題ですので,しっかりと考え方をマスターしましょう!
格子点問題の考え方
格子点
⇒ \(x\) or \(y\) 軸に平行な直線ごとにカウントし,総和(Σ)を考える


解答・解説
(2)解答・解説
\(S=\displaystyle\sum_{k=1}^{n}{k\cdot 2^{k}}\) とおく.
つまり,
\(S=\)\(1\cdot 2\)\(+2\cdot2^2+3\cdot2^3+\cdots+n\cdot2^{n}\) ・・・①
①を \(2\) 倍すると
\(2S=\)\(1\cdot2^2+2\cdot2^3+3\cdot2^4+\cdots+(n-1)\cdot2^{n}\)\(+n\cdot2^{n+1}\) ・・・②
①ー②より
\(-S=\)\(2\)\(+2^2+2^3+\cdots+2^{n}\)\(-n\cdot2^{n+1}\)
\(-S=\displaystyle\frac{2(2^n-1)}{2-1}-n\cdot2^{n+1}\)
よって,\(S=(n-1)\cdot2^{n+1}+2\)
(3)解答・解説
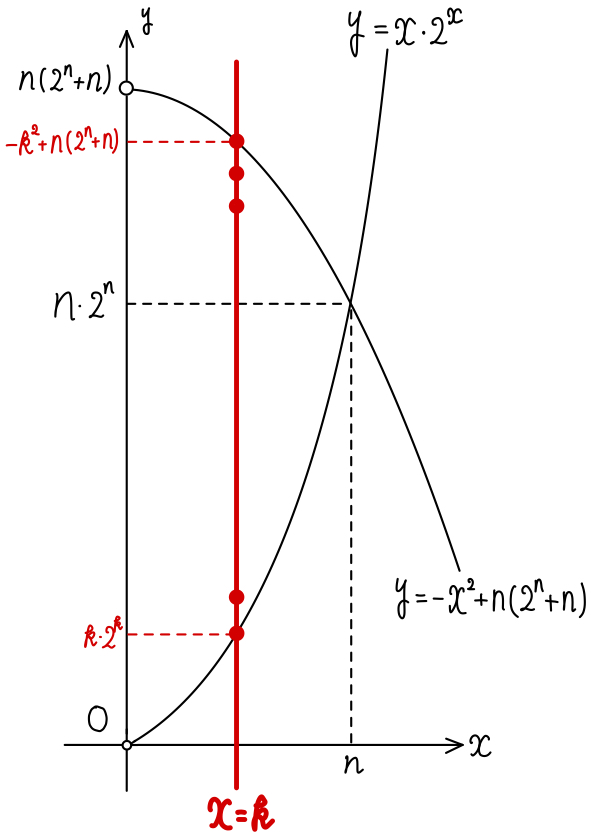
真数条件から \(x>0\) であり,
\(\log_{2}{x}+x=\log_{2}{x\cdot 2^x}\) より
\(y=2^{\log_{2}{x}+x}=2^{\log_{2}{x\cdot 2^x}}=x\cdot 2^x\)
\(D_{n}\) 内において,
直線 \(x=k\) ( \(0<k≦n\),\(k\) は整数 ) 上には
\(-k^2+n(2^n+n)-k\cdot 2^k+1\) 個の格子点があるので
求める格子点の個数は
\(\displaystyle\sum_{k=1}^{n}{\left\{-k^2+n(2^n+n)-k\cdot 2^k+1\right\}}\)
\(=-\displaystyle\frac{1}{6}n(n+1)(2n+1)+n^2(2^n+n)-S+n\)
(2)の結果から \(S=(n-1)\cdot2^{n+1}+2\) より
\(=-\displaystyle\frac{1}{6}n(n+1)(2n+1)+n^2(2^n+n)-\left\{(n-1)\cdot2^{n+1}+2\right\}+n\)
\(=\displaystyle\frac{2}{3}n^3-\displaystyle\frac{1}{2}n^2+\displaystyle\frac{5}{6}n-2+(n^2-2n+2)\cdot 2^n\)








コメント