【2023早稲田大学・理工・第4問】
複素数平面上に \(2\) 点 \(A(1)\),\(B(\sqrt{3}i)\) がある.ただし,\(i\) は虚数単位である.複素数 \(z\) に対し \(w=\displaystyle\frac{3}{z}\) で表される点 \(w\) を考える.以下の問に答えよ.
(1) \(z=1\),\(\displaystyle\frac{1+\sqrt{3}i}{2}\),\(\sqrt{3}i\) のときの \(w\) をそれぞれ計算せよ.
(2) 実数 \(t\) に対し \(z=(1-t)+t\sqrt{3}i\) とする.\(\alpha=\displaystyle\frac{3-\sqrt{3}i}{2}\) について,\(\alpha z\) の実部を求め,さらに \((w-\alpha)\overline{(w-\alpha)}\) を求めよ.
(3) \(w\) と原点を結んでできる線分 \(L\) を考える.\(z\) が線分 \(AB\) 上を動くとき,線分 \(L\) が通過する範囲を図示し,その面積を求めよ.
解答・解説
(1)
\(z=1\) のとき \(w=\displaystyle\frac{3}{1}=3\)
\(z=\displaystyle\frac{1+\sqrt{3}i}{2}\) のとき
\(w=\displaystyle\frac{6}{1+\sqrt{3}i}=\displaystyle\frac{3-3\sqrt{3}i}{2}\)
\(z=\sqrt{3}i\) のときの
\(w=\displaystyle\frac{3}{\sqrt{3}i}=-\sqrt{3}i\)
(2)
\(z=(1-t)+t\sqrt{3}i\) ,\(\alpha=\displaystyle\frac{3-\sqrt{3}i}{2}\) より
\(\alpha z=\left\{(1-t)+t\sqrt{3}i\right\}\times \displaystyle\frac{3-\sqrt{3}i}{2}\)
\(=\left\{\displaystyle\frac{3}{2}(1-t)+\displaystyle\frac{3}{2}t\right\}+\left\{\displaystyle\frac{3\sqrt{3}t}{2}-\displaystyle\frac{\sqrt{3}}{2}(1-t)\right\}i\)
\(=\displaystyle\frac{3}{2}+\left(2\sqrt{3}-\displaystyle\frac{\sqrt{3}}{2}\right)i\)
よって,\(\alpha z\) の実部は \(\displaystyle\frac{3}{2}\)
また,
\((w-\alpha)\overline{(w-\alpha)}\)
\(=(w-\alpha)(\overline{w}-\overline{\alpha})\)
\(=\left(\displaystyle\frac{3}{z}-\alpha\right)\left(\displaystyle\frac{3}{\overline{z}}-\overline{\alpha}\right)\)
\(=\displaystyle\frac{9}{|z|^2}-\displaystyle\frac{3\alpha}{\overline{z}}-\displaystyle\frac{3\overline{\alpha}}{z}+|\alpha|^2\)
\(=-\displaystyle\frac{3}{|z|^2}\left\{\alpha z+\overline{(\alpha z)}-3\right\}+|\alpha|^2\)
\(\alpha z\) の実部は \(\displaystyle\frac{3}{2}\) より,\(\alpha z+\overline{(\alpha z)}=3\)
よって,\((w-\alpha)\overline{(w-\alpha)}=|\alpha|^2\)
\(|\alpha|^2=\left|\displaystyle\frac{3-\sqrt{3}i}{2}\right|^2=\left(\displaystyle\frac{3}{2}\right)^2+\left(-\displaystyle\frac{\sqrt{3}}{2}\right)^2=3\)
したがって,\((w-\alpha)\overline{(w-\alpha)}=3\)
(3)
線分 \(AB\) 上の点は実数 \(t\) を用いて
\(z=(1-t)+t\sqrt{3}i\) ( \(0≦t≦1\) ) と表せる.
\(\alpha=\displaystyle\frac{3-\sqrt{3}i}{2}\) とすると(2)の結果から
\(|w-\alpha|^2=3\)
つまり \(|w-\alpha|=\sqrt{3}\) なので
点 \(w\) は中心が \(\alpha\),半径 \(\sqrt{3}\) の円周上にある.
ここで,\(w=\displaystyle\frac{3}{z}\) より
\(arg w=-arg z\) であり,
\(0≦arg z≦\displaystyle\frac{\pi}{2}\) より
\(-\displaystyle\frac{\pi}{2}≦arg w≦0\) となる.
したがって線分 \(L\) が通過する領域は下図の斜線部になる(ただし境界線を含む).
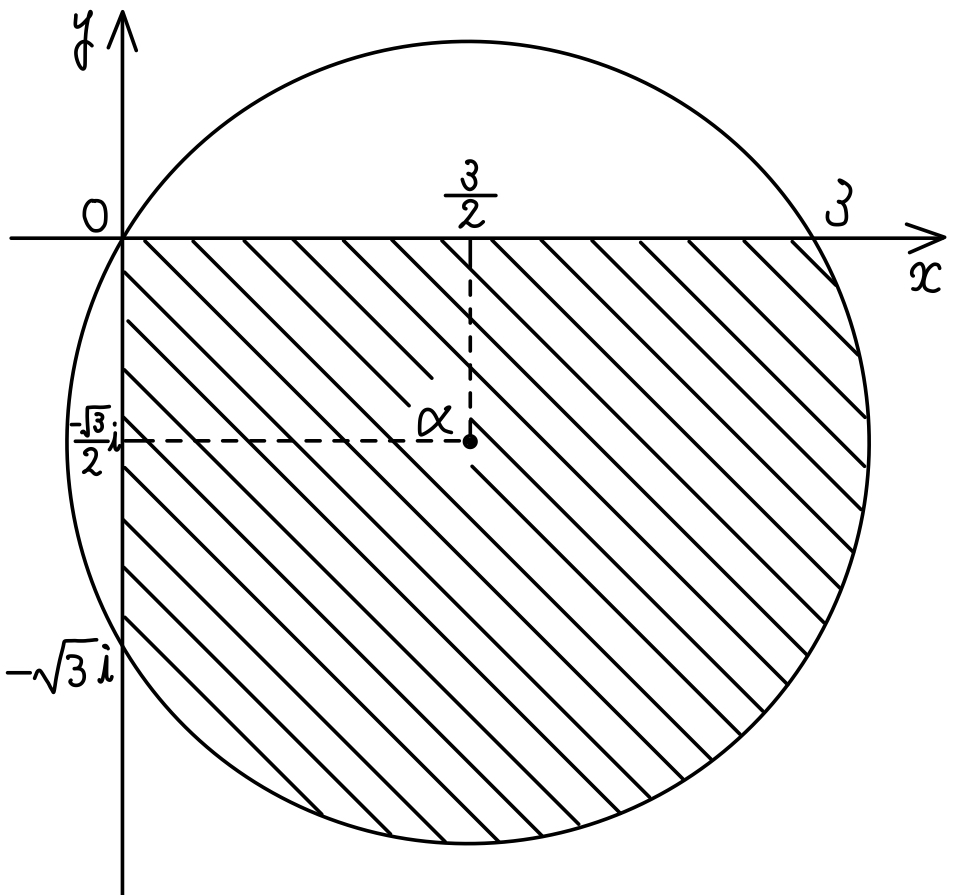
 \(2\) 点 \(3\) と \(-\sqrt{3}i\) の中点が \(\alpha\) より
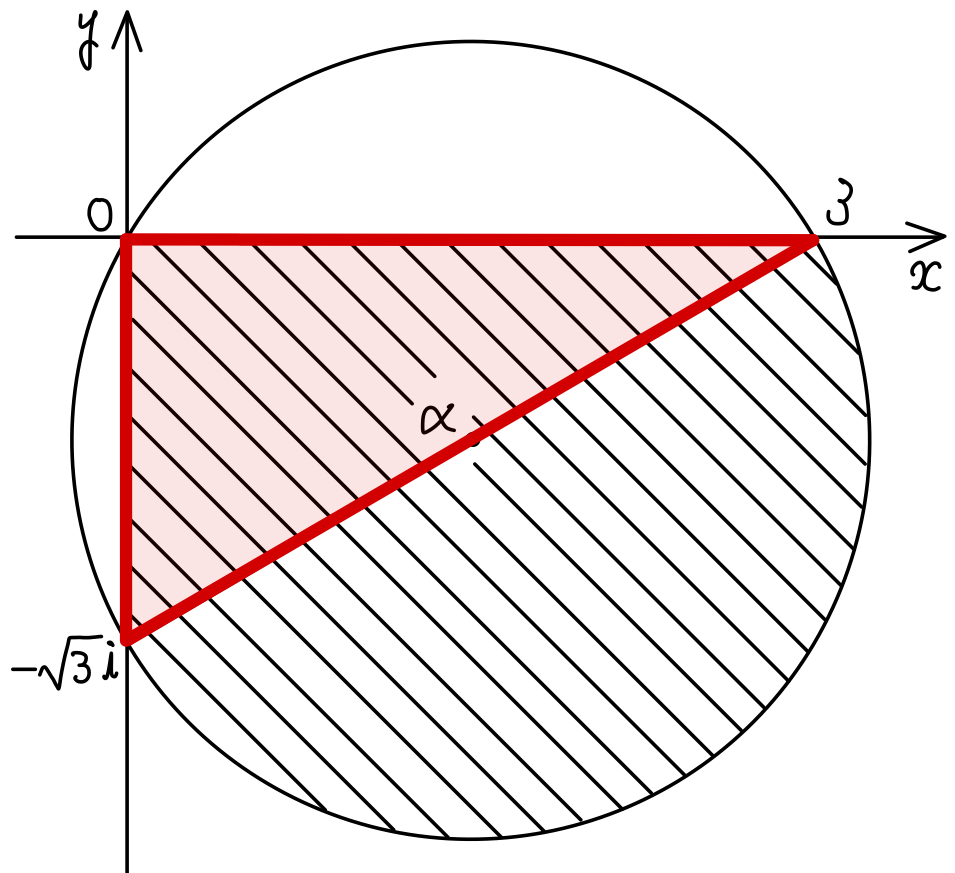
\(2\) 点 \(3\) と \(-\sqrt{3}i\) の中点が \(\alpha\) より
\(2\) 点 \(3\) と \(-\sqrt{3}i\) を結んだ線分は円の直径となる.
求める面積は,直角三角形と半径 \(\sqrt{3}\) の半円の面積の合計であるから,
\(\displaystyle\frac{1}{2}\cdot 3 \cdot\sqrt{3}+\displaystyle\frac{1}{2}\cdot\left(\sqrt{3}\right)^2\cdot\pi=\displaystyle\frac{3\pi}{2}+\displaystyle\frac{3\sqrt{3}}{2}\)







コメント