【2002京都大学】三角関数の解の個数の対応関係｜置き換えによる定数分離(3次関数)

方程式の実数解の個数について

\(2\) 倍角，\(3\) 倍角の公式より

\(\cos 3\theta°=4\cos^3\theta°-3\cos \theta°\) ，\(\cos 2 \theta°=2\cos^2 \theta°-1\) であるから

\(\cos 3\theta°-\cos 2\theta°+3\cos \theta°-1=a\)

\(\iff\) \(a=4\cos^3\theta°-2\cos^2\theta°\) ・・・①

定数分離

①の形より，両辺のグラフの交点を考えてもよいが，

右辺の \(y=4\cos^3\theta°-2\cos^2\theta°\) のグラフは・・・。

( ※ 数学Ⅲの微分を学習すればかけますが大変・・・ )

そこで，次のPointを考えよう！

置き換え&解の個数の対応関係のチェック

例① \(x=\displaystyle\frac{1}{2}\) ( \(x\) の解が \(1\) 個 ) のとき

\(x=\cos \theta°=\displaystyle\frac{1}{2}\)

\(0≦\theta≦360\) において，\(\theta=60，120\) ( \(\theta\) の解は \(2\) 個 )

⇒ \(x\) の解が \(1\) 個のとき，\(\theta\) は解が \(2\) 個

例② \(x=-1\) ( \(x\) の解が \(1\) 個 ) のとき

\(x=\cos \theta°=-1\)

\(0≦\theta≦360\) において，\(\theta=180\) ( \(\theta\) の解は \(1\) 個 )

⇒ \(x\) の解が \(1\) 個のとき，\(\theta\) も解が \(1\) 個

\(x\) の値によって，\(\theta\) の解の個数の対応関係が変わります！

\(x\) がどのようなときに \(1\) 対 \(2\) 対応 ( または \(1\) 対 \(1\) 対応 ) をしているか確認(記述)しましょう！

解答・解説

\(\cos 3\theta°=4\cos^3\theta°-3\cos \theta°\) ，\(\cos 2 \theta°=2\cos^2 \theta°-1\) であるから

\(\cos 3\theta°-\cos 2\theta°+3\cos \theta°-1=a\)

\(\iff\) \(a=4\cos^3\theta°-2\cos^2\theta°\) ・・・①

\(x=\cos \theta°\) とおく．

\(a=4x^3-2x^2\) ( \(-1≦x≦1\) )

ここで \(f(x)=4x^3-2x^2\) とおく．

\(-1≦x≦1\) における \(y=f(x)\) のグラフを考える．

\(f^{\prime}(x)=12x^2-4x=4x(3x-1)\)

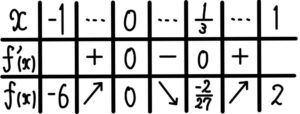
よって，\(-1≦x≦1\) における \(y=f(x)\)

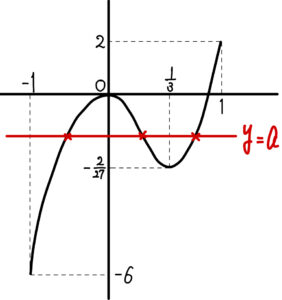のグラフは右図のようになる．

このグラフと直線 \(y=a\) の交点の \(x\) 座標が \(f(x)=a\) の解である．

また， \(x=\pm1\) のときは \(x\) の値が \(1\) 個に \(\theta\) が \(1\) 個，

\(-1<x<1\) のときは \(x\) の値が \(1\) 個に \(\theta\) が \(2\) 個対応する．

したがって，

\(a<-6\) または \(2<a\) のとき  \(0\) 個

\(a=-6 , 2\) のとき \(1\) 個

\(-6<a<-\displaystyle\frac{2}{27}\) または \(0<a<2\) のとき \(2\) 個

\(a=-\displaystyle\frac{2}{27} , 0\) のとき \(4\) 個

\(-\displaystyle\frac{2}{27}<a<0\) のとき \(6\) 個