【2024京都大学・文系・第１問】
四面体 \(OABC\) が次を満たすとする．
\(OA=OB=OC=1\)，\(\angle COA=\angle COB=\angle ACB\)，\(\angle AOB=90°\)
このとき，四面体 \(OABC\) の体積を求めよ．
解答・解説
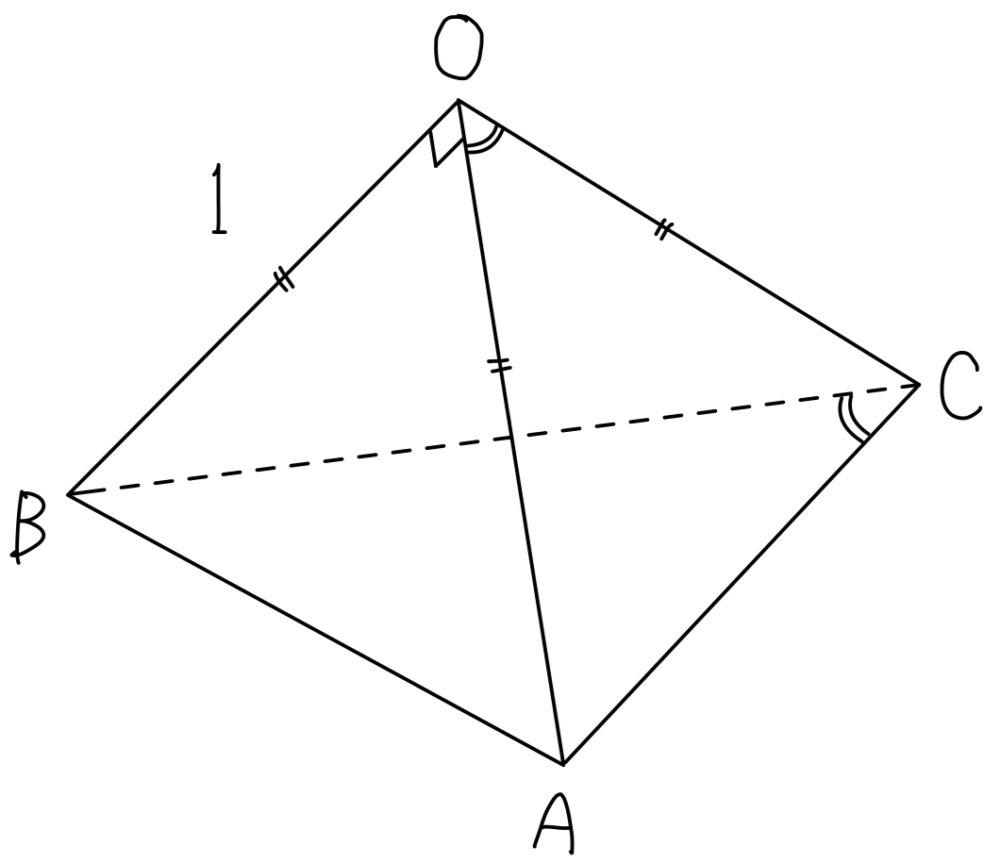\(\triangle OAB\) は \(OA=OB=1\) ，\(\angle AOB=90°\) の直角二等辺三角形より，\(AB=\sqrt{2}\)
また，\(\triangle OAC\) と \(\triangle OBC\) は合同な三角形より \(CA=CB\) かつ
\(\angle ACB=\angle AOC\) であるから
\(\triangle ABC\) と \(\triangle ACO\) は相似な三角形．
\(AC=a\) とおくと
\(AB：AC=AC：AO\) \(\iff\) \(\sqrt{2}：a=a：1\)
\(a^2=\sqrt{2}\)
\(a>0\) より \(a=\sqrt[4]{2}\)
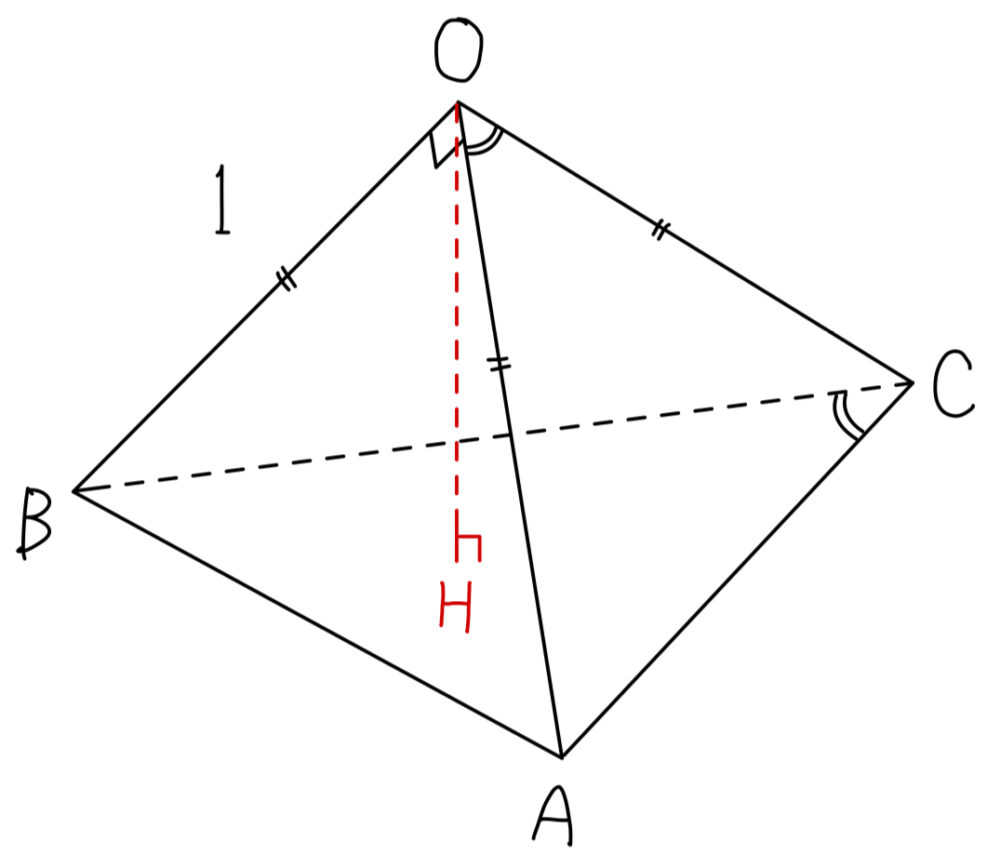次に頂点 \(O\) から \(\triangle ABC\) に垂線 \(OH\) をおろす．
\(OA=OB=OC \)，\(OH\) は共通，\(OH \perp \triangle ABC \) より
\(\triangle OAH≡\triangle OBH≡\triangle OCH \)
よって，\(AH=BH=CH \)
つまり点 \(H\) は \(\triangle ABC\) の外心となる．
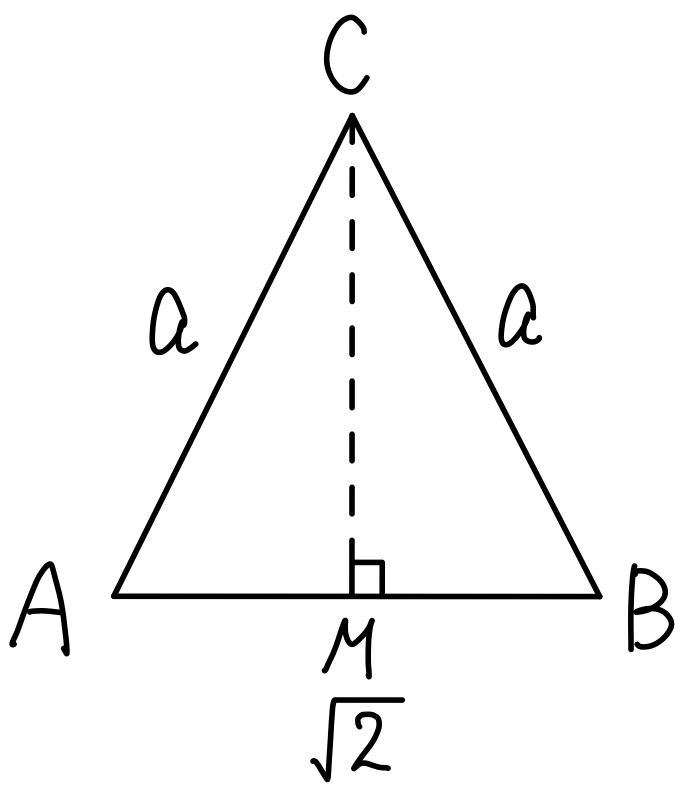ここで \(\triangle ABC\) について
二等辺三角形であることに注目し，\(AB\) の中点を \(M\) とし，\(CM=b\) とおく．
三平方の定理より \(a^2= \left(\displaystyle\frac{\sqrt{2}}{2}\right)^2+b^2\)
\(b^2=\sqrt{2}-\displaystyle\frac{1}{2}\)
また，\(\triangle ACM\) に注目すると
\(\sin\angle CAM=\displaystyle\frac{CM}{AC}=\displaystyle\frac{b}{a}\) であり，
\(\triangle ABC\) で正弦定理より
\(2AH=\displaystyle\frac{a}{\sin\angle CAM}\)
よって，\(AH=\displaystyle\frac{a^2}{2b}\)
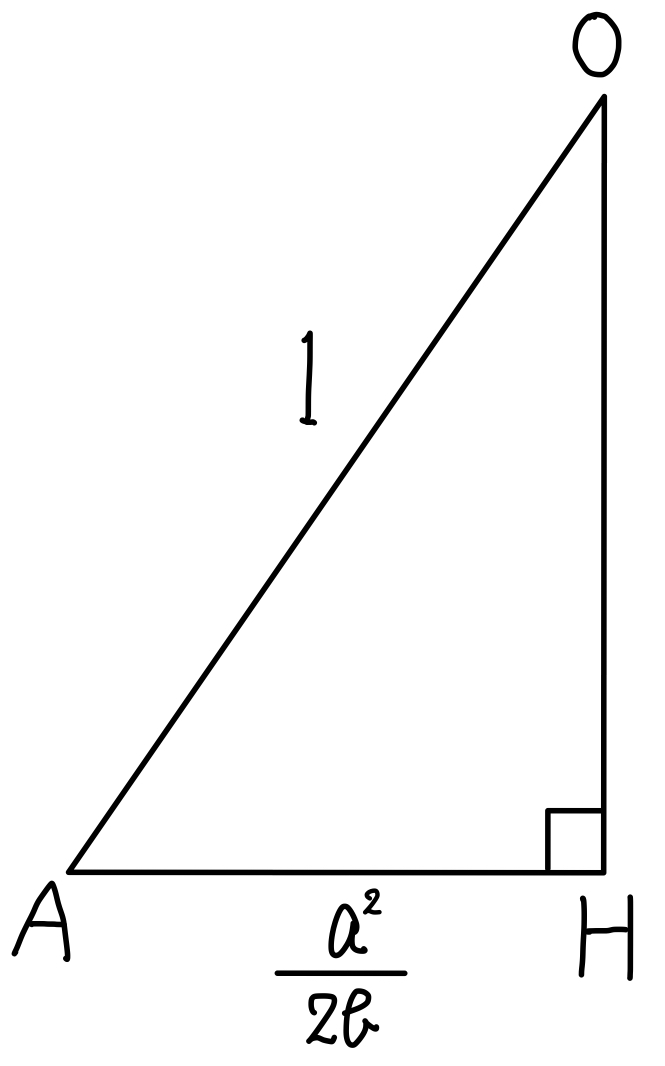\(\triangle OAH\) で三平方の定理から
\(OH^2=1^2-\left(\displaystyle\frac{a^2}{2b}\right)^2=\displaystyle\frac{2b^2-1}{2b^2}\)
\(OH>0\) より \(OH=\sqrt{\displaystyle\frac{2b^2-1}{2b^2}}\)
また，\(\triangle ABC=\displaystyle\frac{1}{2}\times a\times\sqrt{2}\times\sin\angle CAM=\displaystyle\frac{\sqrt{2}}{2}b\) であるから
求める四面体の体積 \(V\) は
\(V=\displaystyle\frac{1}{3}\times\triangle ABC\times OH=\displaystyle\frac{1}{3}\times\displaystyle\frac{\sqrt{2}}{2}b \times\sqrt{\displaystyle\frac{2b^2-1}{2b^2}}\)
\(V=\displaystyle\frac{1}{6}\sqrt{2b^2-1}=\displaystyle\frac{\sqrt{2\sqrt{2}-1}}{6}\)
コメント