【2024京都大学・文系・第5問】
関数 \(y=x^2-4x+5\) のグラフの \(x>1\) の部分を \(C\) とする.このとき,下の条件を満たすような正の実数 \(a\),\(b\) について,座標平面の点 \((a,b)\) が動く領域の面積を求めよ.
「 \(C\) と直線 \(y=ax+b\) は二つの異なる共有点を持つ.」

解答・解説
\(C\):\(y=x^2-4x+5\) (\(x>1\))
\(l\) :\(y=ax+b\) (\(a>0,b>0\))
\( x^2-4x+5=ax+b\)
\(x^2-(a+4)x-b+5=0\)
ここで,\(f(x)= x^2-(a+4)x-b+5\) とおくと
\(C\) と \(l\) が二つの異なる共有点を持つのは
\(f(x)=0\) が \(x>1\) で異なる \(2\) つの実数解をもつことと同値
よって \(f(x)=0\) の判別式を \(D\) とするとき
(ⅰ) \(D>0\) (ⅱ)\(y=f(x)\) の軸 \(>1\) (ⅲ) \(f(1)>0\)
の(ⅰ)~(ⅲ)を満たせばよい.
(ⅰ)\(D=(a+4)^2-4(-b+5)>0\)
よって,\(b>-\displaystyle\frac{1}{4}(a+4)^2+5\) ・・・①
(ⅱ) \(y=f(x)\) の軸は
\(x=\displaystyle\frac{a+4}{2}>1\) \(\iff\) \(a>-2\)
これは \(a>0\) より常に満たす.
(ⅲ) \(f(1)=1-(a+4)-b+5>0\) \(\iff\) \(b<-a+2\) ・・・②
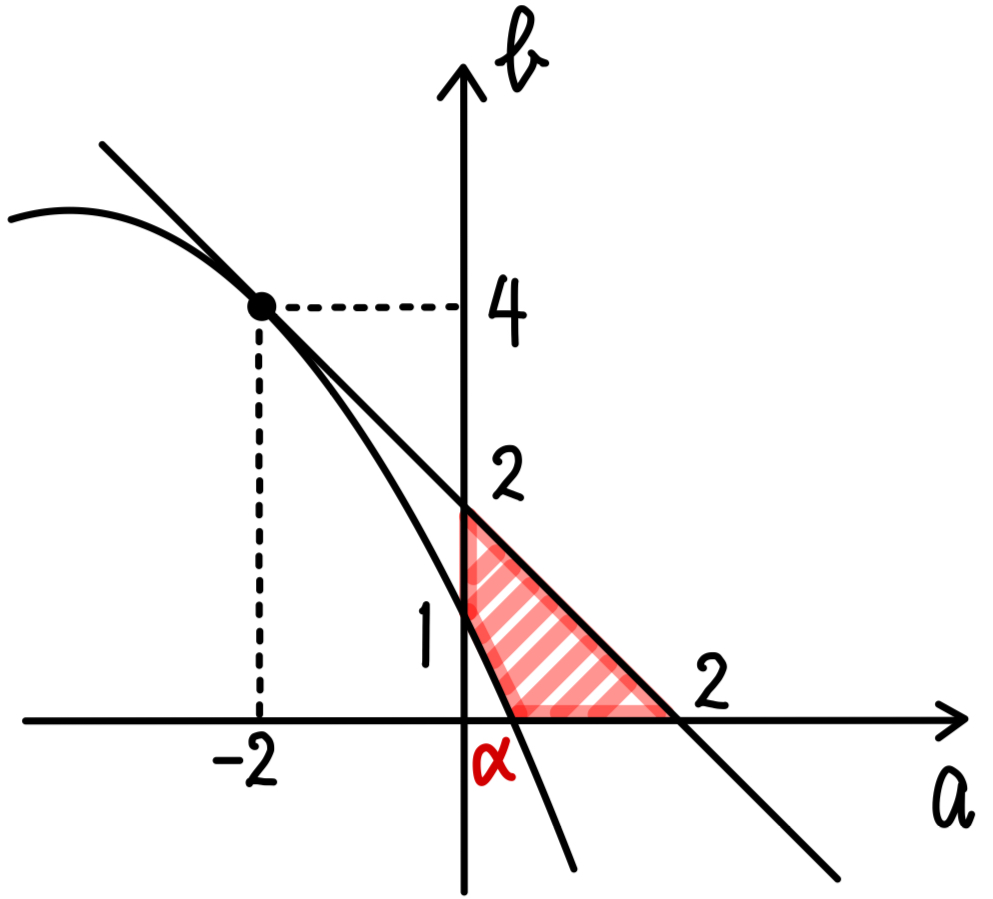
\(b=-\displaystyle\frac{1}{4}(a+4)^2+5\) と \(b=-a+2\) のグラフは \((-2,4)\) で接することに注意して \(a>0\),\(b>0\) の範囲で領域を考えると,右図の斜線部分(境界は含まない)となる.
ここで,\( b=-\displaystyle\frac{1}{4}(a+4)^2+5\) かつ \(b=0\) かつ \(a>0\) を満たす \(a\) の値は \(a=2\sqrt{5}-4\) (\(=\alpha\)とおく)
よって求める領域の面積 \(S\) は
\(S=\displaystyle\frac{1}{2}\cdot 2 \cdot 2-\displaystyle\int^{\alpha}_{0}\left\{-\displaystyle\frac{1}{4}(a+4)^2+5\right\}da\)
\(=2-\Bigl[-\displaystyle\frac{1}{12}(a+4)^3+5a\Bigr]^{\alpha}_{0}\)
\(=2+\displaystyle\frac{1}{12}(\alpha+4)^3-5\alpha-\displaystyle\frac{4^3}{12}\)
\(\alpha=2\sqrt{5}-4\) より
\(S=\displaystyle\frac{50-20\sqrt{5}}{3}\)







コメント