絶対値の方程式・不等式の解き方
タイプ⑴ \(| x の式 |=定数\)
【例題】
① \(| x |=2\)
② \(| x |<2\)
③ \(| x |>2\)
① は原点からの距離が 2 である場所
② は原点からの距離が 2 より近い場所
③ は原点からの距離が 2 より遠い場所
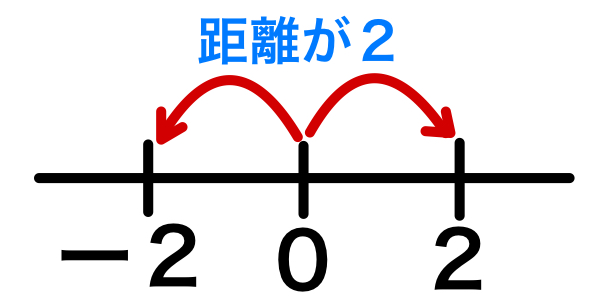
を意味している.
つまり、
① の答えは、\(x=-2 , 2\)
② の答えは、\(-2<x<2\)
③ の答えは、\(x<-2 , 2<x\)
となる.
【例題】
① \(| 2x+1 |=3\)
② \(| 2x+1 |<3\)
①において、\(2x+1=X\) と考えると、
\(| X |=3\) となるため、\(X=-3 , 3\)
つまり、\(2x+1=-3 , 3\)
よって、\(x=-2 , 1\)
②も同様に、\(2x+1=X\) と考えると、
\(| X |<3\) となるため、\(-3<X<3\)
つまり、\(-3<2x+1<3\)
よって、\(-2<x<1\)
タイプ⑵ \(| x の式 | = ( xの式)\)
先ほどのタイプ⑴のように、原点からの距離では処理できない!
理由としては、右辺が \(x\) の式になったためである.
例えば、\(| x の式 | = x \) と言う問題があったとき、
原点からの距離が \(x\) と考えたいが、\(x\) の値がマイナスになる可能性がある.
距離がマイナスと言うのは言うまでもなく無理である・・・
そこでタイプ⑵については、
👉 絶対値の中が正( 0 以上) または負( 0 以上) と場合分け
絶対値の外し方(場合分け)が心配な方は、
を参考に!
【例題】
① \(| x-4 |=3x\)
② \(| x-4 |<3x\)
①の解答
\(| x-4 |=\begin{cases}x-4 (x≧4)\\ -x+4 (x≦4)\end{cases}\) より
(ⅰ) \(x≧4\) のとき
\(x-4=3x\\x=-2\)
しかしこれは \(x≧4\) を満たさないため不適
(ⅱ) \(x≦4\) のとき
\(-x+4=3x\\x=1\)
これは \(x≦4\) を満たす
したがって、\(x=1\)
②の解答
\(| x-4 |=\begin{cases}x-4 (x≧4)\\ -x+4 (x≦4)\end{cases}\) より
( ⅰ ) \(x≦4\) のとき
\(-x+4<3x\\x>1\)
これと \(x≦4\) の共通部分を考えると、
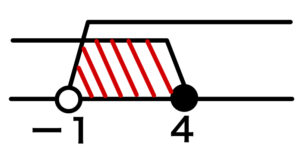
\(1<x≦4\)
( ⅱ ) \(x≧4\) のとき
\(x-4<3x\\x>-2\)
これと \(x≧4\) の共通部分を考えると、
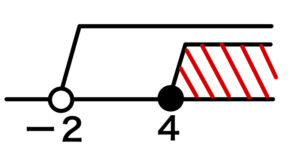
\(x≧4\)
(ⅰ)と(ⅱ)の和集合をとると、
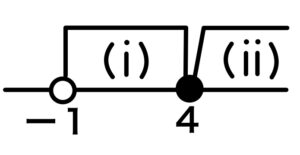
\(1<x\)
タイプ⑶ 複数個の絶対値
【例題】\(| x-1 | + | x-2 | =x\) を解け.
\(| x-1 |\) は \(x=1\) を境に、絶対値の場合分けを行った.
\(| x-2 |\) は \(x=2\) を境に、絶対値の場合分けを行った.
よって、\(x≦1 , 1≦x≦2 , 2≦x\) の 3 つに場合分けをして考える.
(ⅰ) \(x≦1\) のとき
\(| x-1 |=-x+1\)、\(| x-2 |=-x+2\) より
与式は、\(-x+1-x+2=x\)
\(x=1\)
これは \(x≦1\) を満たす
(ⅱ) \(1≦x≦2\) のとき
\(| x-1 |=-x+1\)、\(| x-2 |=x-2\) より
与式は、\(-x+1+x-2=x\)
\(x=-1\)
これは \(1≦x≦2\) を満たさないため不適
(ⅲ) \(2≦x\) のとき
\(| x-1 |=x-1\)、\(| x-2 |=x-2\) より
与式は、\(x-1+x-2=x\)
\(x=3\)
これは \(2≦x \) を満たす
したがって、\(x= 1 , 3\)
最後に
絶対の計算は、定期考査では頻出テーマ。
絶対値の中で場合分けを行う流れは、完全パターン!
しっかりと解法の流れを覚え、演習をしていきましょう!







コメント