
【2021 信州大学 教育学部 第2問】

(1)解答
(1) \(\angle{AOB}=\displaystyle\frac{\pi}{12}\) より
\(\sin \angle{AOB}=\sin \displaystyle\frac{\pi}{12}\)
\(\sin^{2}\displaystyle\frac{\pi}{12}=\displaystyle\frac{1-\cos \displaystyle\frac{\pi}{6}}{2}= \displaystyle\frac{2-\sqrt{3}}{4} \)
\(\sin \displaystyle\frac{\pi}{12}>0\) より
\(\sin \displaystyle\frac{\pi}{12}=\displaystyle\frac{\sqrt{2-\sqrt{3}}}{2}\)
ここで
\(\sqrt{2-\sqrt{3}}=\sqrt{\displaystyle\frac {4-2\sqrt{3}}{2}}=\sqrt{\displaystyle\frac{(\sqrt{3}-1)^2}{2}}=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{2}\)
したがって、
\(\sin \displaystyle\frac{\pi}{12}=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}\)
よって \(\triangle OAB=\displaystyle\frac{1}{2} \cdot 1^2 \cdot \displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}\\=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{8}\)
(2)解答
(2) 面積に注目すると、
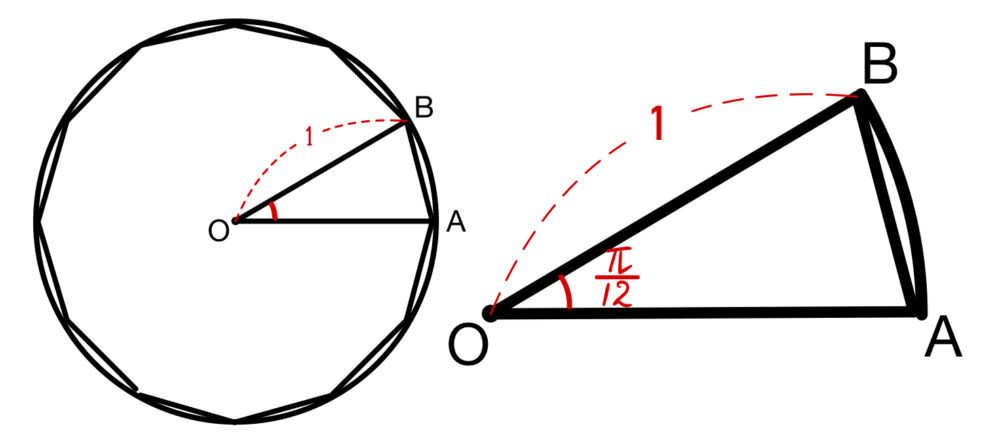
扇形\(OAB>\)\(\triangle OAB\) ・・・ ①
扇形\(OAB=\displaystyle\frac{1}{2}\cdot 1^2 \cdot \displaystyle\frac{\pi}{12}=\displaystyle\frac{\pi}{24}\)
(1)の結果と①から、
\(\displaystyle\frac{\pi}{24}>\displaystyle\frac{\sqrt{6}-\sqrt{2}}{8}\)
したがって、\(\pi>3(\sqrt{6}-\sqrt{2})\)
2003年 東京大学
2003年の東京大学の問題で、
「円周率が \(3.05\) よりも大きいことを証明せよ.」
はとても有名ですね。
何気なく使用する円周率に関する良問です。有名な問題だからこそ、解法の流れを経験し、類題に対応できるように!








コメント