\(\sin 1\)、\(\sin 2\)、\(\sin 3\) の大小関係を答えよ.
\(1\) ラジアンとは?
度「°」を用いて表す方法を、度数法と言いました.
これは、直角の \(90\) 分の \(1\) を \(1\) 度として表す方法.
それに対して、
図のように、点 \(O\) を中心とする半径 \(1\) の円と半直線 \(OX\)、\(OP\) の交点を、それぞれ\(A\)、\(B\) とする.
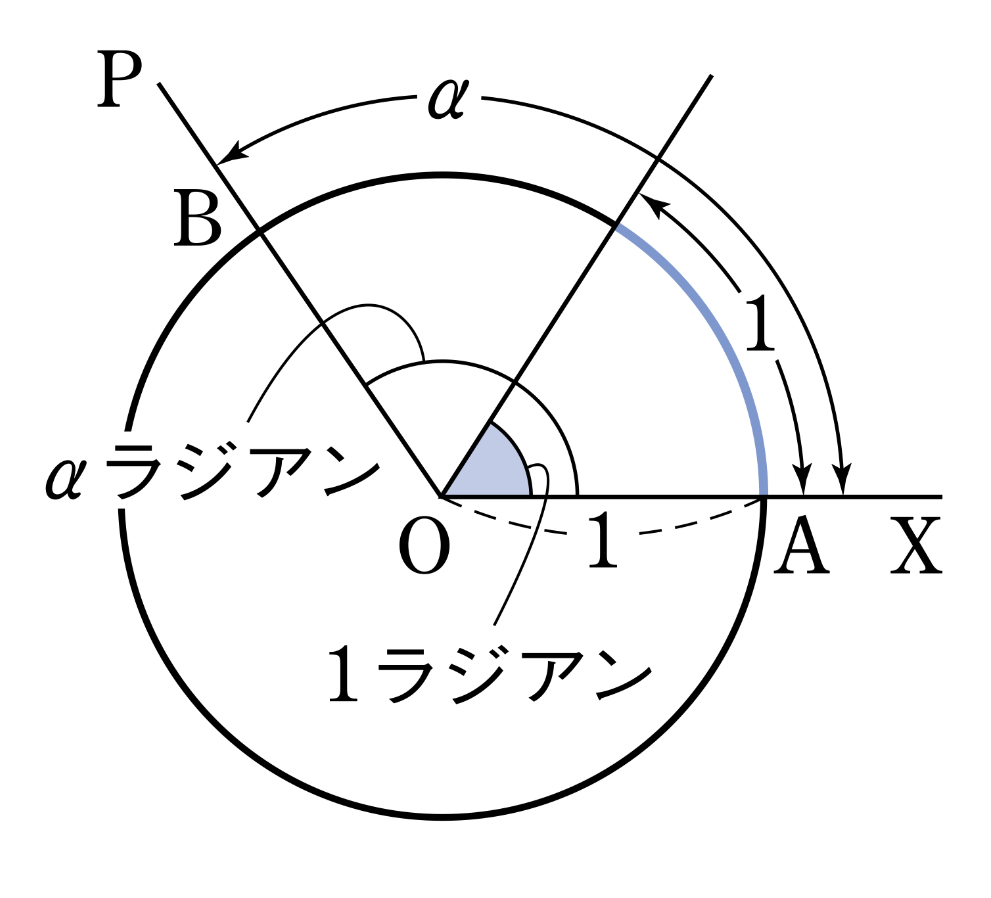
このとき、\(∠XOP\) の大きさは弧 \(AB\) の長さに比例することに注目し、
弧 \(AB\) の長さが \(1\) になるような角を、\(1\) ラジアンという.
例えば、\(∠XOP\) が \(180\text{°}\) のとき、弧 \(AB\) の長さは \(\pi\) であるから、
\(180\text{°}=\pi\) ラジアン
よって、
\(1\) ラジアン \(=\left(\displaystyle\frac{180}{\pi}\right) \text{°}≒57.3\text{°}\)
このような角の大きさの表し方を弧度法という.
\(\sin 1\)、\(\sin 2\)、\(\sin 3\) の大小関係
\(\displaystyle\frac{\pi}{4}<1<\displaystyle\frac{\pi}{3}\)、
\(\displaystyle\frac{\pi}{2}<2<\displaystyle\frac{2\pi}{3}\)、
\(\displaystyle\frac{5\pi}{6}<3<\pi\) より図の単位円において考えると、
\(\sin\) は高さを表すので
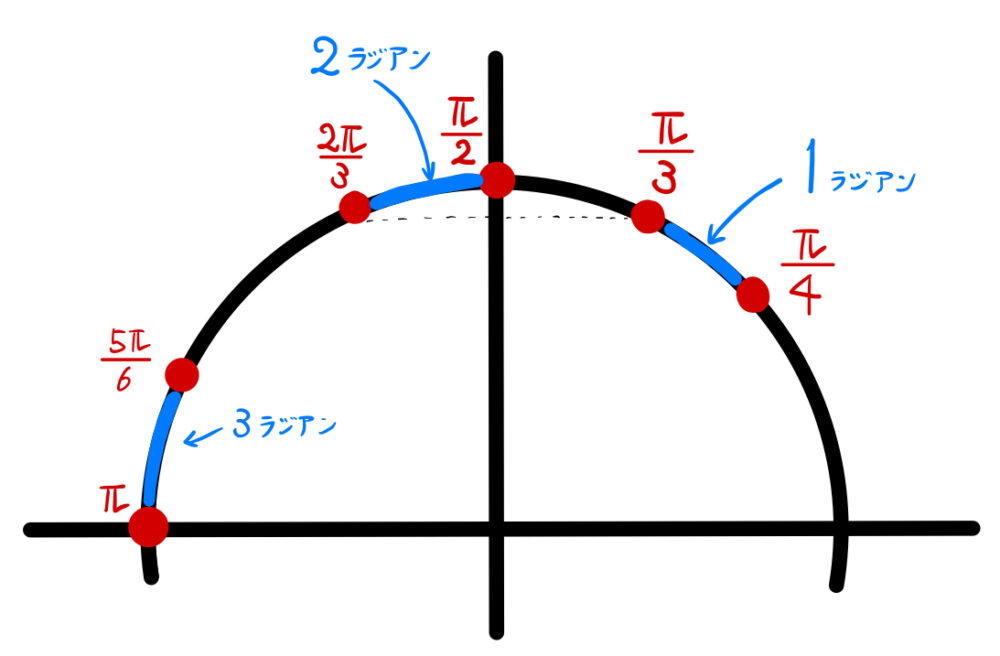
\(\sin 2 > \sin 1 > \sin 3\)
リンク







コメント