2021年共通テスト(数学ⅠA)第4問[整数]
(1)問題と解説

さいころを投げて、偶数の目が \(x\) 回、奇数の目が \(y\) 回でるとき、
偶数の目が \(1\) 回出ると \(5\) 進み、奇数の目が \(1\) 回出ると \(-3\) 進むと考える.
\(x+y=5\) かつ \(5x-3y=1\) を解いて
\(x=2\)、\(y=3\) ・・・〈ア、イ〉
(2)問題と解答
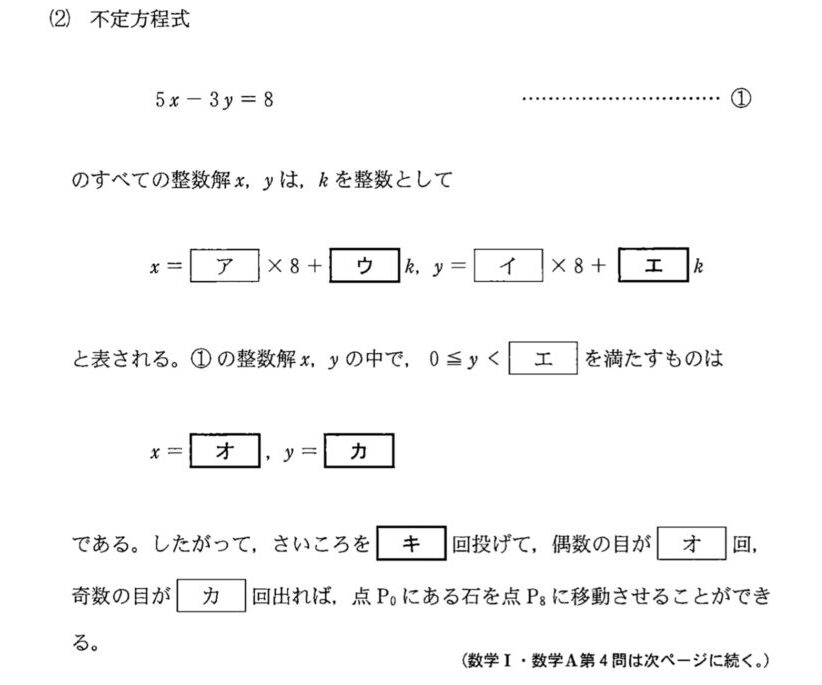
(1)より、\(5\times2-3\times3=1\) を \(8\) 倍して、
\(5\times16-3\times24=8\) より、
①の解の \(1\) つは、\(x=16\)、\(y=24\)
また①より、\(y=\displaystyle\frac{5}{3}x-8\)
つまり、傾きが \(\displaystyle\frac{5}{3}\) の直線と考えて格子点に注目すると、
\(k\) を整数として
\(x=16+3k\)、\(y=24+5k\) ・・・〈ウ、エ〉
\(y=24+5k\) かつ \(0≦y<5\) を満たす整数 \(k=-4\) であるから、
このとき、\(x=4\)、\(y=4\) ・・・〈オ、カ〉
したがって、\(x+y=8\) 回 ・・・〈キ〉


(3)問題と解答

(2)において、\(8\) 回よりも少ない回数で、点 \(P_{0}\) にある石を点 \(P_{8}\) に移動させる方法を考える.
\(8-15=-7\) より、
\(5x-3y=-7\) かつ \(x+y<8\) を満たす整数 \(x\)、\(y\) を考えれば良いので、
これを満たす整数は \(x=1\)、\(y=4\)
つまり、偶数の目が \(1\) 回 ・・・〈ク〉、奇数の目が \(4\) 回 ・・・〈ケ〉
よって、さいころを投げる回数はが、\(1+4=5\) 回 ・・・〈コ〉のときである
(4)問題と解答

・ \(P_{10}\) のとき
\(5x-3y=10\) または \(5x-3y=-5\) かつ \(x+y\) が最小となる正の整数 \(x\)、\(y\) を考えると
\((x,y)=(2,0)\) または \((2,5)\)
つまり、最小回数 ( \(x+y\) が最小となる ) のは、\(2\) 回
・ \(P_{11}\) のとき
\(5x-3y=11\) または \(5x-3y=-4\) かつ \(x+y\) が最小となる正の整数 \(x\)、\(y\) を考えると
\((x,y)=(4,3)\) または \((1,3)\)
つまり、最小回数 ( \(x+y\) が最小となる ) のは、\(4\) 回
・ \(P_{12}\) のとき
\(5x-3y=12\) または \(5x-3y=-3\) かつ \(x+y\) が最小となる正の整数 \(x\)、\(y\) を考えると
\((x,y)=(3,1)\) または \((0,1)\)
つまり、最小回数 ( \(x+y\) が最小となる ) のは、\(1\) 回
・ \(P_{13}\) のとき
\(5x-3y=13\) または \(5x-3y=-2\) かつ \(x+y\) が最小となる正の整数 \(x\)、\(y\) を考えると
\((x,y)=(5,4)\) または \((2,4)\)
つまり、最小回数 ( \(x+y\) が最小となる ) のは、\(6\) 回
・ \(P_{14}\) のとき
\(5x-3y=14\) または \(5x-3y=-1\) かつ \(x+y\) が最小となる正の整数 \(x\)、\(y\) を考えると
\((x,y)=(4,2)\) または \((1,2)\)
つまり、最小回数 ( \(x+y\) が最小となる ) のは、\(3\) 回
したがって、最小回数が最も多いのは、点 \(P_{13}\) の ③ ・・・〈サ〉であり、
その最小回数は \(6\) 回 ・・・〈シ〉









コメント