次の問に答えよ.
(1) 次の条件Aをみたす座標平面上の点 \( x , y \) 全体の集合を図示せよ.
条件A:すべての実数 \(t\) に対して \(y≧tx-2t^2\) が成立する.
(2) 次の条件Bをみたす座標平面上の点 \( x , y \) 全体の集合を図示せよ.
条件B: \(| t |≦1\) をみたすすべての実数 \(t\) に対して \(y≧tx-2t^2\) が成立する.
![]()
Point・考え方・方針
おさえておきたいPoint2つ!
ある範囲において \(f(x)≧0\)
☞ (ある範囲における \(f(x)\) の最小値) \(≧0\)
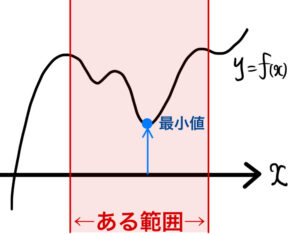
例えば上図のような \(y=f(x)\) を考える.
「ある範囲において \(f(x)≧0\)」であるとは、
「ある範囲で \(y=f(x)\) が \(x\) 軸より上側にある 」
と言う状態を表す.
「ある範囲で \(y=f(x)\) が \(x\) 軸より上側にある 」ことを言うためには、
「\(y=f(x)\) の最小値が \(x\) 軸より上側にある」ことが言えればよい.
すべての 〇〇 に対して・・・
☞ 〇〇 の関数と考える.
方針
(1) すべての実数 \(t\) に対して・・・より、
\(t\) の関数と考える.(\(x , y \) は定数扱い)
すべての項を左辺に移行し、\(t\) について降べきの順に並べると、
\(2t^2-xt+y≧0\)
左辺を \(f(t)\) とおくと(1)の問題は、
『 すべての実数 \(t\) に対して \(f(t)≧0\) が成立する.』
つまり \(t\) の 2 次関数として考え、
すべての実数 \(t\) に対して、 \(f(t)\) の最小値が \(0\) 以上になることを考えればよい.
(2)については、\(t\) の範囲が \(-1≦t≦1\) となるので、
\(-1≦t≦1\) において、 \(f(t)\) の最小値が \(0\) 以上になることを考えればよい.
【最重要】軸・範囲が動く2次関数の最大値・最小値の場合分けに不安がある人は、
解答
(1) \(f(t)=2t^2-xt+y\) とおく.
すべての実数 \(t\) に対して、 \(f(t)\) の最小値が \(0\) 以上になることを考えればよい.
\(f(t)=2\displaystyle\left(t-\displaystyle\frac{x}{4}\right)^2-\displaystyle\frac{x^2}{8}+y\) より
\(-\displaystyle\frac{x^2}{8}+y≧0\)
よって、\(y≧\displaystyle\frac{x^2}{8}\)
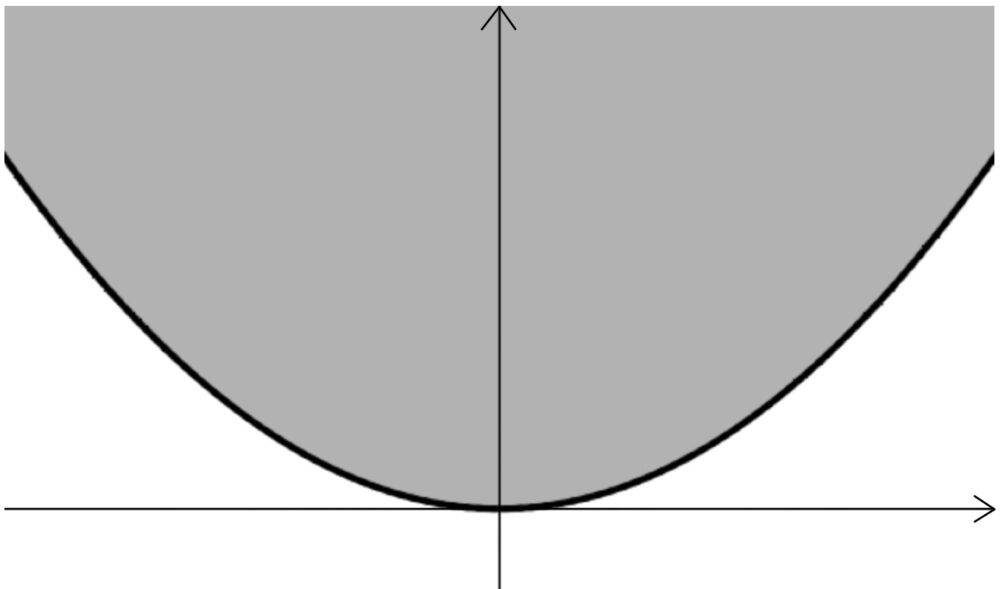
ただし、境界線は含む
(2) \(-1≦t≦1\) において、 \(f(t)\) の最小値が \(0\) 以上になることを考えればよい.
\(f(t)=2\displaystyle\left(t-\displaystyle\frac{x}{4}\right)^2-\displaystyle\frac{x^2}{8}+y\) より
(ア) \(\displaystyle\frac{x}{4}<-1\) \(\iff\) \(x<-4\) のとき
\(f(-1)=2+x+y≧0\) \(\iff\) \(y≧-x-2\) ・・・①
(イ) \(-1≦\displaystyle\frac{x}{4}≦1\) \(\iff\) \(-4≦x≦4\) のとき
\(f(\displaystyle\frac{x}{4})=-\displaystyle\frac{x^2}{8}+y≧0\) \(\iff\) \(y≧\displaystyle\frac{x^2}{8}\) ・・・②
(ウ) \(1<\displaystyle\frac{x}{4}\) \(\iff\) \(4<x\) のとき
\(f(1)=2-x+y≧0\) \(\iff\) \(y≧x-2\) ・・・③
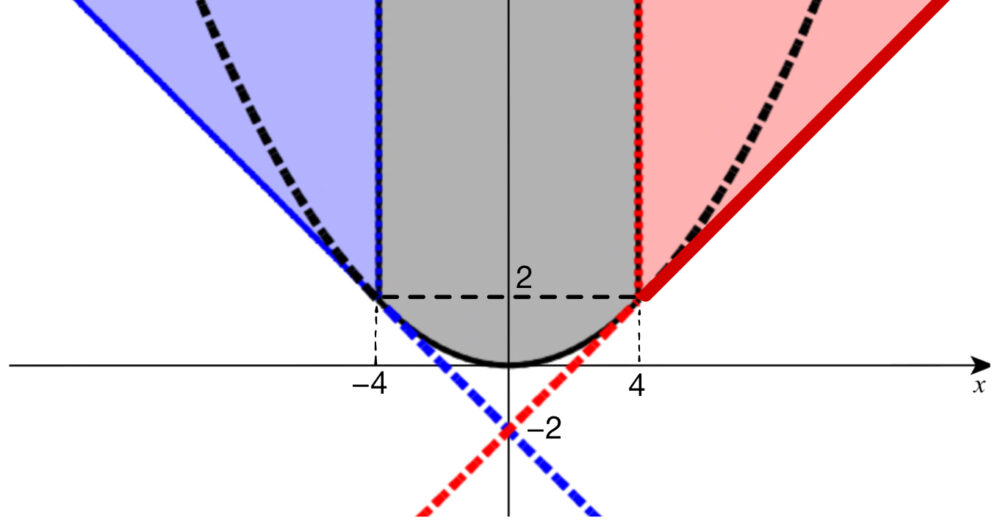
ただし、境界線は含む
(※(ア)は青の領域、(イ)は黒の領域、(ウ)は赤の領域を表している)
類題演習
今回のテーマのPointは、関数の問題において最頻出・超重要問題です。
本問では結果的に 2 次関数として扱いましたが、3 次関数など(数学Ⅲでは何でもあり)形を変えて出題されます.また不等式の証明としても利用できるので、しっかりと考え方をおさえましょう!
類題として










コメント