【例題:(数学 Ⅱ)4STEEP238】
直線 \(y=ax+b\) は \(2\) 点 \(P ( 1 , -1 )\) , \(Q ( 2 , 1 )\) の間を通る.ただし, \(P\) と \(Q\) は通らないものとする.このとき,点 \(( a , b )\) の存在範囲を求めよ.
正領域・負領域とは?
平面上の曲線 \(f(x,y)=0\) において,平面は \(2\) つに分けられる.このとき,
\(f(x,y)>0\) となる領域を正領域,\(f(x,y)<0\) となる領域を負領域 という.
《例①》\(f(x,y)=2x-y-1\) のとき

正領域は,\(f(x,y)=2x-y-1>0\)
\(\iff\) \(y<2x-1\) を表す領域になり,
負領域は,\(f(x,y)=2x-y-1<0\)
\(\iff\) \(y>2x-1\) を表す領域となる.
これらを図示すると右図のようになる.

注意!「正領域は上側!」
といった間違ったイメージを持たないように!
与式によってどちらにでもなり得ます。
《例②》\(f(x,y)=x^2+y^2-1\) のとき
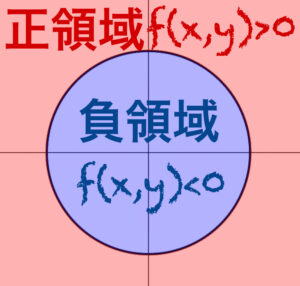 正領域は,\(f(x,y)=x^2+y^2-1>0\)
正領域は,\(f(x,y)=x^2+y^2-1>0\)
\(\iff\) \(x^2+y^2>1\) を表す領域になり,
負領域は,\(f(x,y)=x^2+y^2-1<0\)
\(\iff\) \(x^2+y^2<1\) を表す領域となる.
これらを図示すると右図のようになる.
例題(数学 Ⅱ:4STEEP238)解答・解説
直線 \(y=ax+b\) は \(2\) 点 \(P ( 1 , -1 )\) , \(Q ( 2 , 1 )\) の間を通る.ただし, \(P\) と \(Q\) は通らないものとする.このとき,点 \(( a , b )\) の存在範囲を求めよ.
考え方
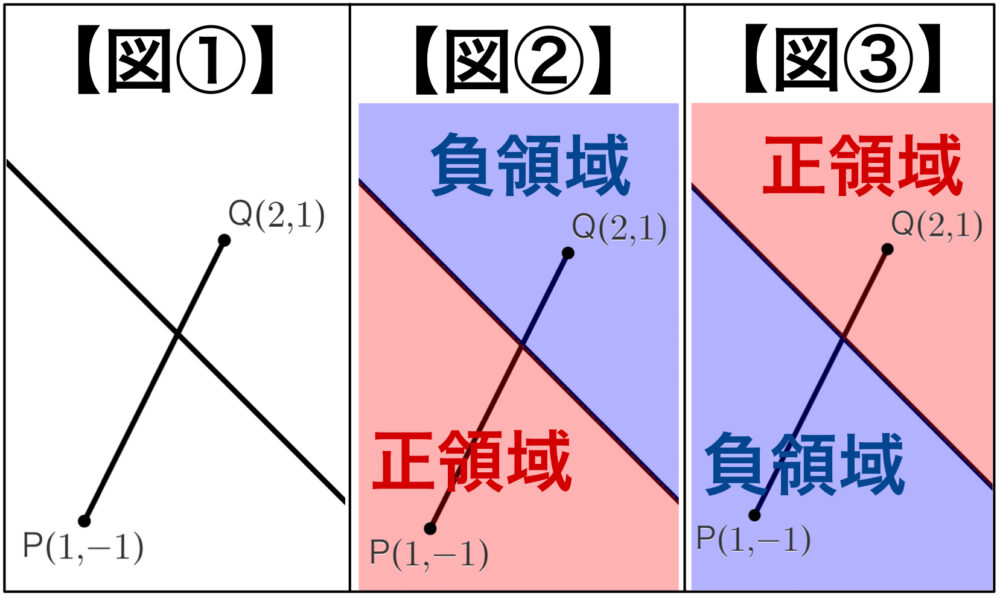
題意は,【図①】のような状況になれば良いという問題です.
つまり,直線 \(y=ax+b\) \(\iff\) \(ax-y+b=0\) によって分けられた \(2\) つの領域の一方に点 \(P ( 1 , -1 )\) が,他方に点 \(Q ( 2 , 1 )\) があればよい.
つまり,【図②】や【図③】のように一方が正領域,他方が負領域にあることになる.
これを式で表すと,\(f(x,y)=ax-y+b\) とおくとき
【図②】は \(f( 1 , -1 )>0\) かつ \(f( 2 , 1 )<0\)
【図③】は \(f( 1 , -1 )<0\) かつ \(f( 2 , 1 )>0\)
【図②】または【図③】となれば良いので,これらをまとめると,
解答
\(f(x,y)=ax-y+b\) とおく.
題意を満たすためには,\(f(1,-1)\times f(2,1)<0\) を考えれば良い
\(f(1,-1)\times f(2,1)=(a+1+b)(2a-1+b)<0\)
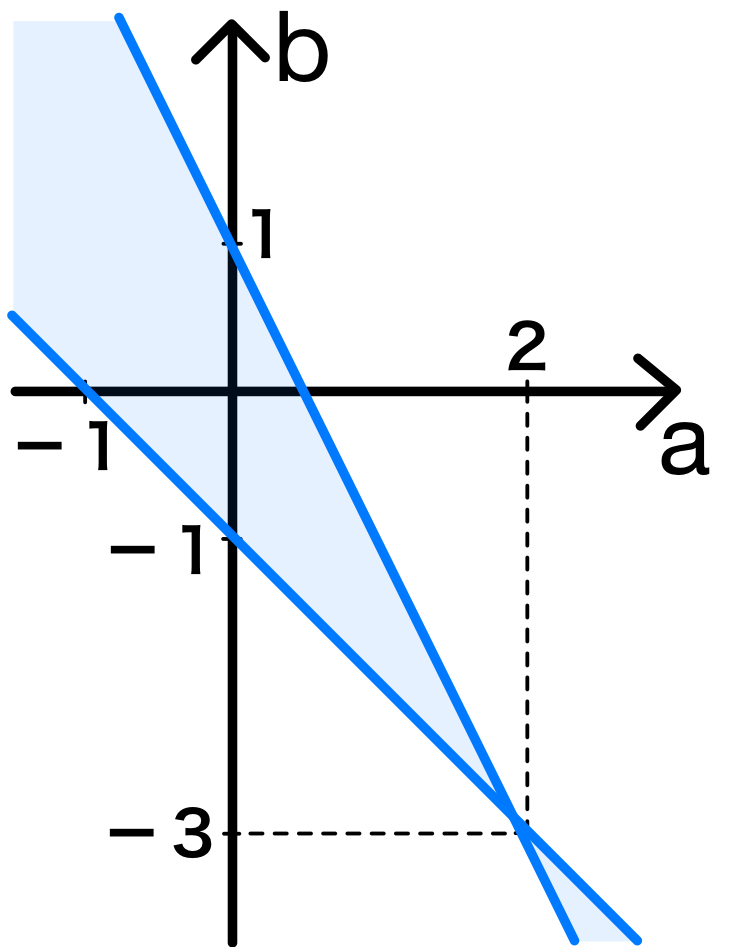
よって,\((b+a+1)(b+2a-1)<0\) ・・・①
ここで,\(b=-a-1\) と \(b=-2a+1\) の交点は \((2 , -3)\) であり,それぞれの直線を図示し領域を考えると,求める領域は下図.ただし,境界線は含まない.







コメント