【2010神戸大学・文(一部)】
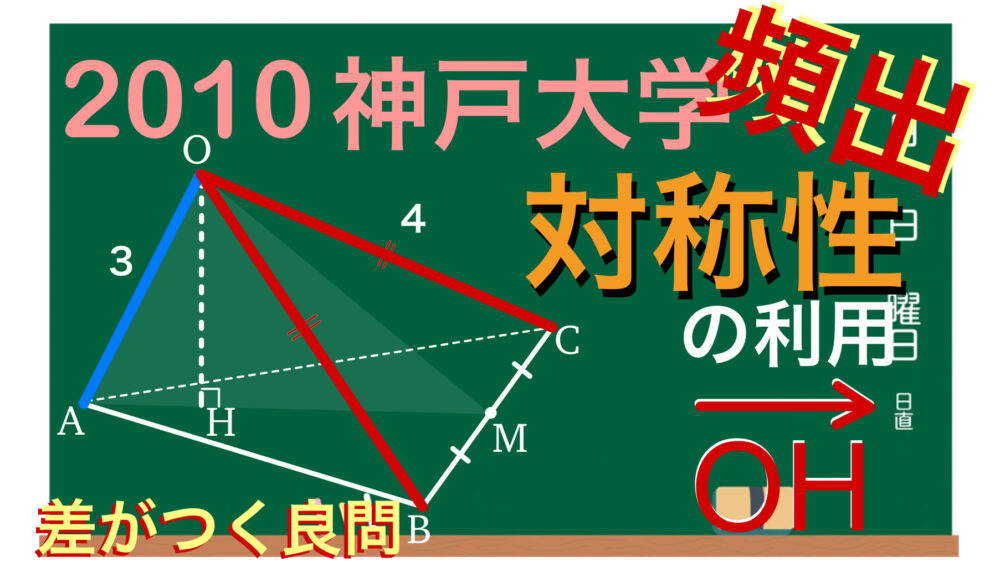
空間内に \(4\) 点 \(O\) , \(A\) , \(B\) , \(C\) があり，
\(OA=3\) , \(OB=OC=4\) , \(\angle BOC=\angle COA=\angle AOB=\displaystyle\frac{\pi}{3}\)
であるとする．\(3\) 点 \(A\) , \(B\) , \(C\) を通る平面に垂線 \(OH\) をおろす．
\(\overrightarrow{a}=\overrightarrow{OA}\) , \(\overrightarrow{b}=\overrightarrow{OB}\) , \(\overrightarrow{c}=\overrightarrow{OC}\) とし，
\(\overrightarrow{OH}=r\overrightarrow{a}+s\overrightarrow{b}+t\overrightarrow{c}\)
と表すとき， \(r\) , \(s\) , \(t\) を求めよ．
考え方・ポイント
Point：対称性の利用
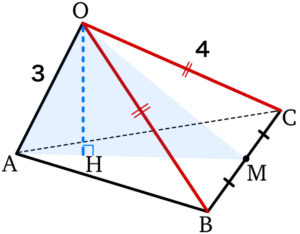まず初めに，問題の条件(図)を見て意識してほしいことが，図形の『対称性』についてである．
\(OB=OC=4\) , \(\angle AOB=\angle AOC=\displaystyle\frac{\pi}{3}\) , \(OA\) は共通であるから，
\(\triangle OAB≡\triangle OAC\) である．
このことから，線分 \(BC\) の中点を \(M\) としたとき，
四面体 \(OABC\) は，平面 \(OAM\) に関して対称な立体であることがわかる．
対象性から，\(s=t\) であることが分かり，文字数を\(1\) つ減らすことができた！
どうしてこんなこととに気がつけるの？？
ただの偶然？？
気がつけるかどうかではなく，疑ってかかるように意識しましょう！
作問者としては，適当な数字で問題を作っているわけではありません！意図的な値に設定していることが多く，対称性のある図形の問題は多くは出題されています！
文字数を\(1\) 文字でも減らせると後々の計算が楽になるから，最初に考える習慣を身につけます！
共面条件
共面条件とは，異なる \(4\) 点が同一平面上に並ぶときの条件
（※ \(4\) 点が同一直線状であるときは除く）
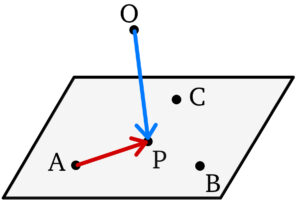\(4\) 点 \(A\)，\(B\)，\(C\)， \(P\) が同一平面上にあるとき
① \(A\) を始点として考える( \(k\)，\(l\) は実数 )
\(\overrightarrow{AP}=k\overrightarrow{AB}+l\overrightarrow{AC}\)
② \(O\) を始点として考える( \(s\)，\(t\)，\(u\) は実数 )
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\) かつ \(s+t+u=1\)
垂直条件
平面 \(\alpha\) 上の異なる \(2\) つのベクトル \(\overrightarrow{x}\) , \(\overrightarrow{y}\) ( ただし，\(\overrightarrow{x}\) , \(\overrightarrow{y}\) は零ベクトルでなく，互いに平行ではない ) に対して，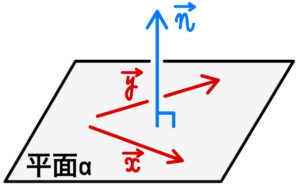
平面 \(\alpha\) \(\perp \overrightarrow{n}\)
\(\iff\) \(\overrightarrow{x} \perp \overrightarrow{n}\) かつ \(\overrightarrow{y} \perp \overrightarrow{n}\)
\(\iff\) \(\overrightarrow{x}\cdot\overrightarrow{n}=0\) かつ \(\overrightarrow{y}\cdot\overrightarrow{n}=0\)
共面条件，垂直条件を用いた頻出な有名問題の演習は「【頻出】四面体の体積｜空間ベクトル(共面条件・垂直条件)」
解答
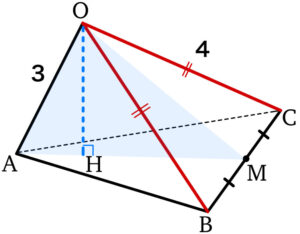\(\overrightarrow{a}\cdot\overrightarrow{b}=3\cdot 4\cdot \cos \displaystyle\frac{\pi}{3}=6\) ,
\(\overrightarrow{b}\cdot\overrightarrow{c}=4\cdot 4\cdot \cos \displaystyle\frac{\pi}{3}=8\) ,
\(\overrightarrow{c}\cdot\overrightarrow{a}=4\cdot 3\cdot \cos \displaystyle\frac{\pi}{3}=6\) .
\(OB=OC=4\) , \(\angle AOB=\angle AOC=\displaystyle\frac{\pi}{3}\) , \(OA\) は共通であるから，
\(\triangle OAB≡\triangle OAC\) である．
このことから，線分 \(BC\) の中点を \(M\) としたとき，
四面体 \(OABC\) は，平面 \(OAM\) に関して対称な立体であり，
対称性から \(s=t\) ・・・① を満たす．
①より
\(\overrightarrow{OH}=r\overrightarrow{a}+s\overrightarrow{b}+s\overrightarrow{c}\)
とおける．このとき，点 \(H\) は平面 \(ABC\) 上であるから
\(r+s+s=1\) \(\iff\) \(r+2s=1\) ・・・②
共面条件②の「係数の和が \(1\) 」になることを利用した
また \(OH \perp\) 平面 \(ABC\) より， \(\overrightarrow{OH} \perp \overrightarrow{AB}\)
つまり \(\overrightarrow{OH}\cdot \overrightarrow{AB}=0\)
よって，\((r\overrightarrow{a}+s\overrightarrow{b}+s\overrightarrow{c})(\overrightarrow{b}-\overrightarrow{a})=0\)
これを計算してまとめると \(r=4s\) ・・・③
②，③より，\(r=\displaystyle\frac{2}{3}\) , \(s=t=\displaystyle\frac{1}{6}\)
したがって，\(\overrightarrow{OH}=\displaystyle\frac{2}{3}\overrightarrow{a}+\displaystyle\frac{1}{6}\overrightarrow{b}+\displaystyle\frac{1}{6}\overrightarrow{c}\)
コメント