【2020数学ⅡB：第３問数列】

(１)，(２)ー①問題と解答・解説《ア〜キ》

(１)，(２)ー①問題と解答・解説《ア〜キ》

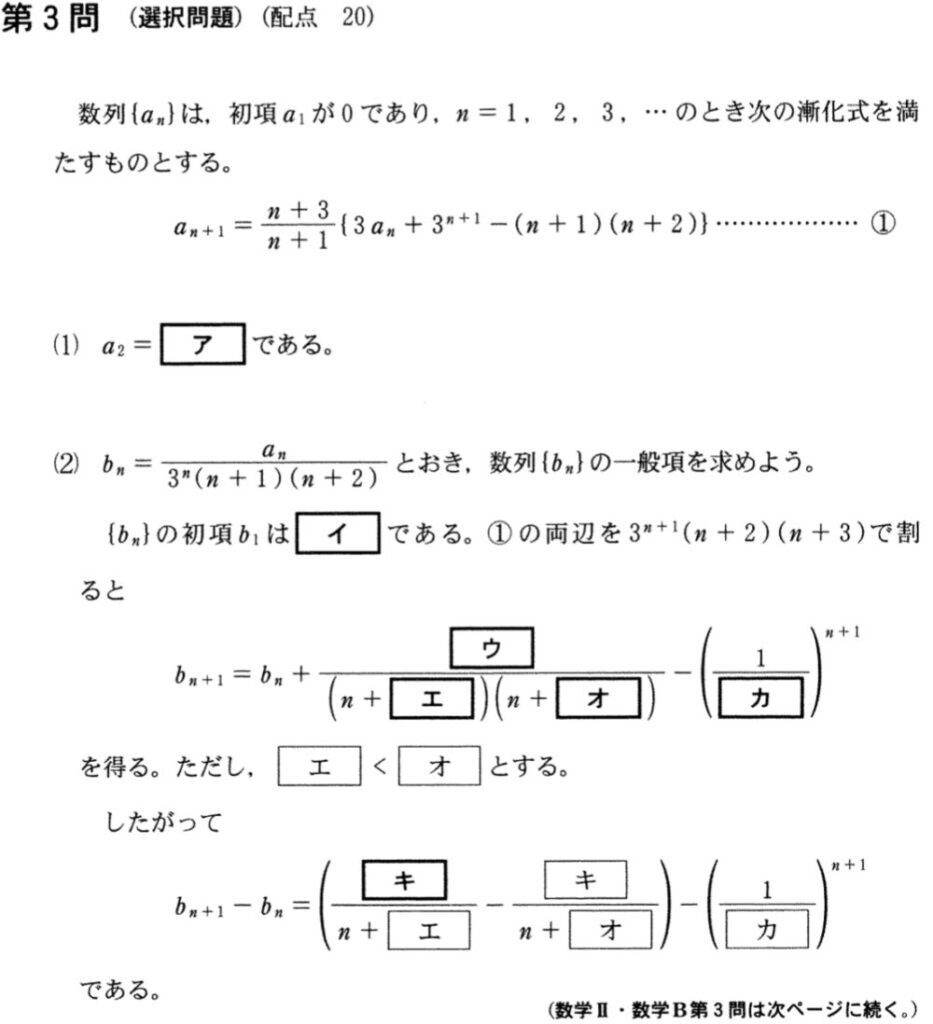
(１)　\(a_{n+1}=\displaystyle\frac{n+3}{n+1}\left\{3a_{1}+3^{n+1}-(n+1)(n+2)\right\}\) ・・・①

①に \(n=1\) を代入して

\(a_{2}=\displaystyle\frac{4}{2}(3a_{1}+3^2-2\cdot3)=\)\(6\) ・・・《ア》

(２)　\(b_{n}=\displaystyle\frac{a_{n}}{3^n(n+1)(n+2)}\) とおくと，\(a_{1}=0\) より

\(b_{1}=\displaystyle\frac{a_{1}}{3\cdot2\cdot3}=\)\(0\) ・・・《イ》

①の両辺を \(3^{n+1}(n+2)(n+3)\) で割ると

\(\displaystyle\frac{a_{n+1}}{3^{n+1}(n+2)(n+3)}=\displaystyle\frac{1}{3^{n+1}(n+2)(n+3)}\cdot\displaystyle\frac{n+3}{n+1}\left\{3a_{1}+3^{n+1}-(n+1)(n+2)\right\}\)

\(\displaystyle\frac{a_{n+1}}{3^{n+1}(n+2)(n+3)}=\displaystyle\frac{a_{n}}{3^n(n+1)(n+2)}+\displaystyle\frac{1}{(n+1)(n+2)}-\displaystyle\frac{1}{3^{n+1}}\)

よって，\(b_{n+1}=b_{n}+\displaystyle\frac{1}{(n+1)(n+2)}-\left(\displaystyle\frac{1}{3}\right)^{n+1}\) ・・・《ウ〜カ》

\(\displaystyle\frac{1}{(n+1)(n+2)}=\displaystyle\frac{1}{n+1}-\displaystyle\frac{1}{n+2}\) であるから，

したがって，\(b_{n+1}-b_{n}=\left(\displaystyle\frac{1}{n+1}-\displaystyle\frac{1}{n+2}\right)-\left(\displaystyle\frac{1}{3}\right)^{n+1}\) ・・・《キ》

階差数列の漸化式のパターンに帰着したね！

漸化式が不安な方は「【漸化式】有名・頻出13パターン解法まとめ｜数学B数列」を参考に！

(２)ー②問題と解答・解説《ク〜チ》

(２)ー②問題と解答・解説《ク〜チ》

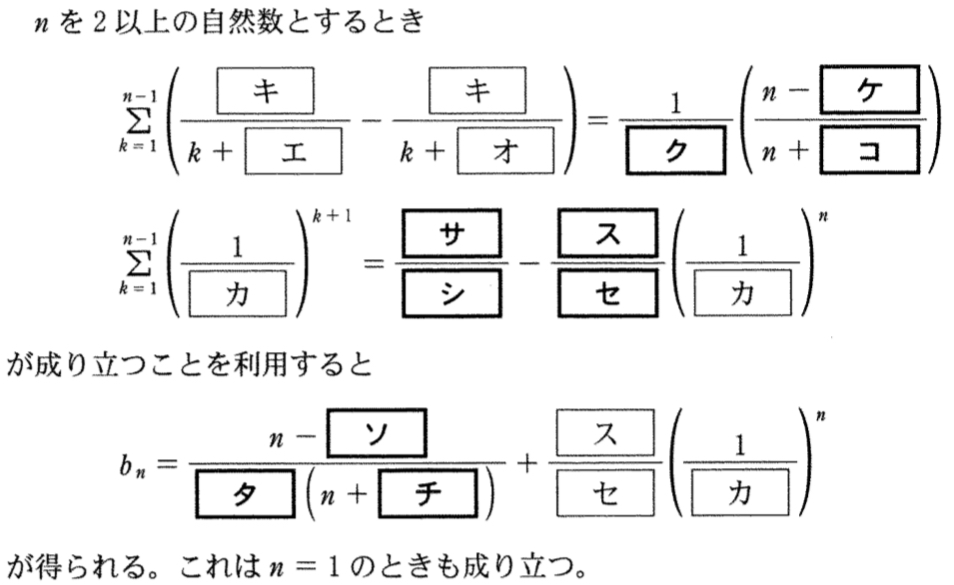
\(n\) を \(2\) 以上の自然数とするとき

\(\displaystyle\sum_{k=1}^{n-1}{\displaystyle\frac{1}{k+1}-\displaystyle\frac{1}{k+2}}\)

\(=\left(\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}\right)+\left(\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}\right)+\left(\displaystyle\frac{1}{4}-\displaystyle\frac{1}{5}\right)+\cdots+\left(\displaystyle\frac{1}{n}-\displaystyle\frac{1}{n+1}\right)\)

\(=\displaystyle\frac{1}{2}-\displaystyle\frac{1}{n+1}\)

\(=\displaystyle\frac{1}{2}\left(\displaystyle\frac{n-1}{n+1}\right)\) ・・・《ク〜コ》

また，\(\displaystyle\sum_{k=1}^{n-1}{\left(\displaystyle\frac{1}{3}\right)}^{k+1}\) は

初項： \(\displaystyle\frac{1}{9}\) , 公比： \(\displaystyle\frac{1}{3}\) , 項数： \(n-1\) の等比数列の和であるから

\(\displaystyle\sum_{k=1}^{n-1}{\left(\displaystyle\frac{1}{3}\right)}^{k+1}=\displaystyle\frac{\displaystyle\frac{1}{9}\left\{1-\left(\displaystyle\frac{1}{3}\right)^{n-1}\right\}}{1-\displaystyle\frac{1}{3}}\)

\(=\displaystyle\frac{1}{6}-\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{3}\right)^n\) ・・・《サ〜セ》

\(b_{n+1}-b_{n}=\left(\displaystyle\frac{1}{n+1}-\displaystyle\frac{1}{n+2}\right)-\left(\displaystyle\frac{1}{3}\right)^{n+1}\) より，

\(n≧2\) のとき

\(b_{n}=b_{1}+\displaystyle\sum_{k=1}^{n-1}{\left(\displaystyle\frac{1}{k+1}-\displaystyle\frac{1}{k+2}\right)-\left(\displaystyle\frac{1}{3}\right)^{k+1}}\) であり \(b_{1}=0\) から

\(b_{n}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{n-1}{n+1}\right)-\left\{\displaystyle\frac{1}{6}-\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{3}\right)^2\right\}\)

よって，\(b_{n}=\displaystyle\frac{n-2}{3(n+1)}+\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{3}\right)^2\) ・・・③ 《ソ〜チ》

これは \(n=1\) のときも成り立つ．

(３)問題と解答・解説《ツ〜ヌ》

(３)問題と解答・解説《ツ〜ヌ》

\(a_{n}=3^n(n+1)(n+2)b_{n}\) であるから，(２)の③に代入して

\(a_{n}=3^n(n+1)(n+2)b_{n}\left\{\displaystyle\frac{n-2}{3(n+1)}+\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{3}\right)^2\right\}\)

よって，\(a_{n}=3^{n-1}(n^2-4)+\displaystyle\frac{(n+1)(n+2)}{2}\) ・・・④《ツ〜ヌ》

(４)問題と解答・解説《ネ〜ヒ》

(４)問題と解答・解説《ネ〜ヒ》

\(n\) が自然数のとき，\(3^{n-1}(n^2-4)\) は \(3\) の倍数であるから，\(a_{n}\) を \(3\) で割った余りは

\(\displaystyle\frac{(n+1)(n+2)}{2}\) を \(3\) で割った余りに等しい．

( ⅰ )　\(n=3k\) のとき

\(\displaystyle\frac{(3k+1)(3k+2)}{2}=\displaystyle\frac{9k^2+9k+2}{2}=\displaystyle\frac{9k(k+1)}{2}+1\)

\(k(k+1)\) は連続する \(2\) つの整数の積であるから \(2\) の倍数でとなるので，\(\displaystyle\frac{9k(k+1)}{2}\) は \(9\) の倍数となる．

よって，\(a_{3k}\) を \(3\) で割った余りは \(1\) ・・・《ネ》

( ⅱ )　\(n=3k+1\) のとき

\(\displaystyle\frac{(3k+2)(3k+3)}{2}=\displaystyle\frac{3(k+1)\left\{k+(2(k+1))\right\}}{2}=3\left\{\displaystyle\frac{k(k+1)}{2}+(k+1)^2\right\}\)

( ⅰ )と同様に \(\displaystyle\frac{k(k+1)}{2}\) は整数であるので，これは常に \(3\) の倍数となる．

よって，\(a_{3k+1}\) を \(3\) で割った余りは \(0\) ・・・《ノ》

( ⅲ )　\(n=3k+2\) のとき

\(\displaystyle\frac{(3k+3)(3k+4)}{2}=\displaystyle\frac{3(k+1)\left\{k+2(k+2)\right\}}{2}=3\left\{\displaystyle\frac{k(k+1)}{2}+(k+1)(k+2)\right\}\)

( ⅱ )と同様に，これも常に \(3\) の倍数となる．

よって，\(a_{3k+2}\) を \(3\) で割った余りは \(0\) ・・・《ハ》

上では記述でも使える解説をしましたが、

答えを求めるだけ(マーク形式)であれば、具体的な値から答えを考えることで時間短縮ができます！

例えば、

\(a_{1}=0\) であり，\(a_{1}\) は \(a_{3k+1}\) に含まれるため、 \(3\) で割った余りは \(0\) であるとわかる．

同様に、\(a_{2}=6\) であることから，\(a_{3k+2}\) を \(3\) で割った余りは \(0\) であることがわかる．

したがって，\(a_{n}\) を \(3\) で割った余りは

\(0\) , \(0\) , \(1\) , \(0\) , \(0\) , \(1\) , \(0\) , \(0\) , \(1\) , \(\cdots\) となる．

よって， \(9\) 項ずつの和を \(3\) で割った余りは \(0\) となるため，

\(2020=9\times 224+4\) であるから，

\(\displaystyle\sum_{k=1}^{n}{a_{k}}\) を \(3\) で割った余りは，\(a_{2017}+a_{2018}+a_{2019}+a_{2020}\) を \(3\) で割った余りとなる．

以上より求める余りは，\(0+0+1+0=\)\(1\) ・・・《ヒ》