【2021早稲田大学・教育】
座標平面上の \(2\) つの曲線 \(y=ae^x\) , \(y=-x^2+2x\) が共有点をもち,かつ,その共有点において共通の接線をもつような正の定数 \(a\) の値を求めよ.
共通接線の解法・考え方
【タイプ⑴】共有点あり
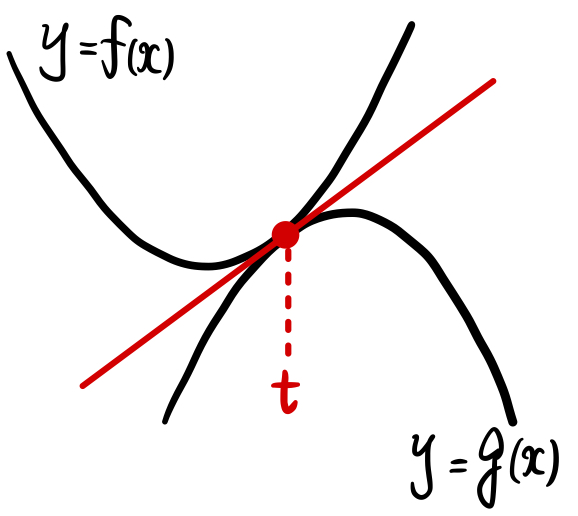
《解法の流れ》
共有点の \(x\) 座標を \(t\) とおくと
\(f(t)=g(t)\) 《 \(y\) 座標の一致》
\(f^{\prime}(t)=g^{\prime} (t)\) 《 接線の傾きの一致》

本問は【タイプ(1)】の共有点があるタイプです!
参考として,共有点がない【タイプ(2)】もセットで確認しておきましょう!
【タイプ(2)】共有点なし
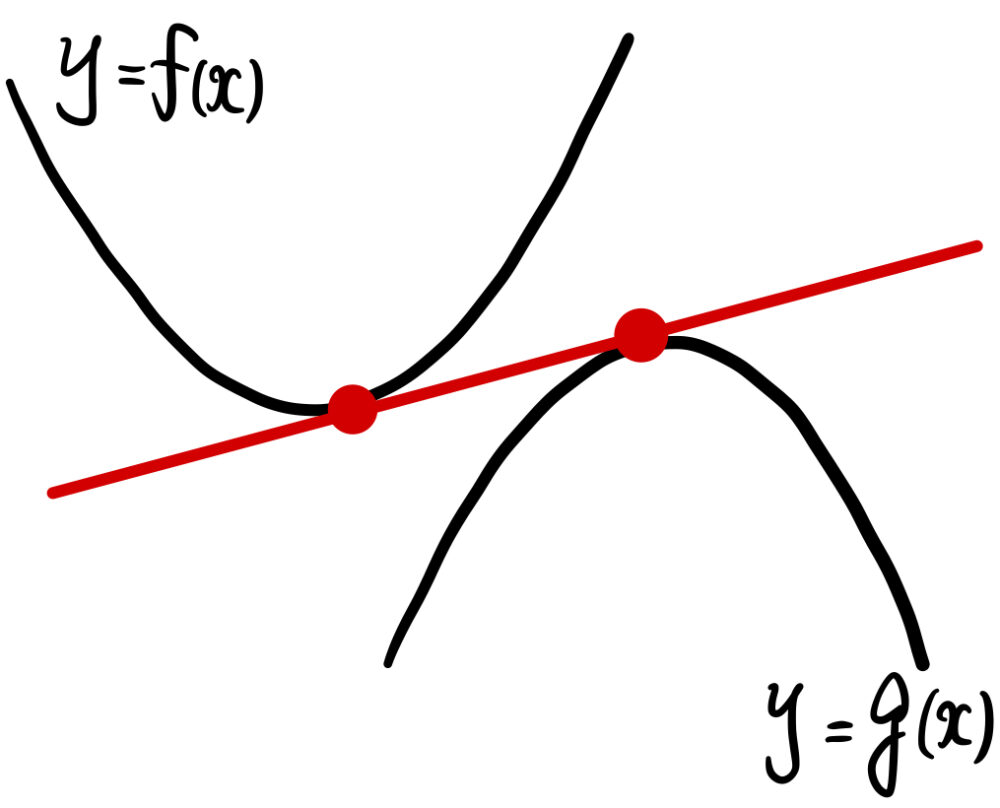
《解法の流れ》
[解法①]
一方の曲線に接点を与え、接線の方程式を求める.
その接線が、他方の曲線と接する条件を考える.
[解法②]
それぞれの曲線に接点を与え、それぞれ接線の方程式を求める.
その 2 接線が一致する条件を考える.
それぞれの解法のメリット・デメリット

解答・解説
【2021早稲田大学・教育】
座標平面上の \(2\) つの曲線 \(y=ae^x\) , \(y=-x^2+2x\) が共有点をもち,かつ,その共有点において共通の接線をもつような正の定数 \(a\) の値を求めよ.
\(f(x)=ae^x\) , \(g(x)=-x^2+2x\) とおき,
\(y=f(x)\) , \(y=g(x)\) の共有点の \(x\) 座標を \(p\) とする.
共通接線をもつ条件は,
\(f(p)=g(p)\) かつ \(f^{\prime}(p)=g^{\prime}(p)\)
\(f(p)=g(p)\) より
\(ae^p=-p^2+2p\) ・・・①
\(f^{\prime}(p)=g^{\prime}(p)\) より
\(ae^p=-2p+2\) ・・・②
①,②より \(-p^2+2p=-2p+2\)
\(p^2-4p+2=0\)
\(p=2\pm\sqrt{2}\)
ここで,\(a>0\) , ②より
\(ae^p=-2p+2>0\)
\(p<1\) となるので,\(p=2-\sqrt{2}\)
②より
\(ae^{2-\sqrt{2}}=-2(2-\sqrt{2})+2=2\sqrt{2}-2\)
したがって,\(a=(2\sqrt{2}-2)e^{\sqrt{2}-2}\)








コメント