【2022関西医科大学・医学部・第2問】
関数 \(f(x)\) を \(f(x)=\displaystyle\frac{6x^2+17x+10}{3x-2}\) と定めるとき,以下の設問に答えよ.
(1) \(f(x)>0\) を満たす \(x\) の値を範囲求めよ.
(2) \(f(x)=Ax+B+\displaystyle\frac{C}{3x-2}\) が \(x\) についての恒等式となるように,定数 \(A\),\(B\),\(C\) の値を定めよ.
(3) \(f(n)\) の値が正の整数となるような整数 \(n\) をすべて求めよ.
解答・解説
(1) \(f(x)>0\) を満たす \(x\) の範囲
\(f(x)>0\) の両辺に \((3x-2)^2\) をかけると,
\((6x^2+17x+10)(3x-2)>0\)
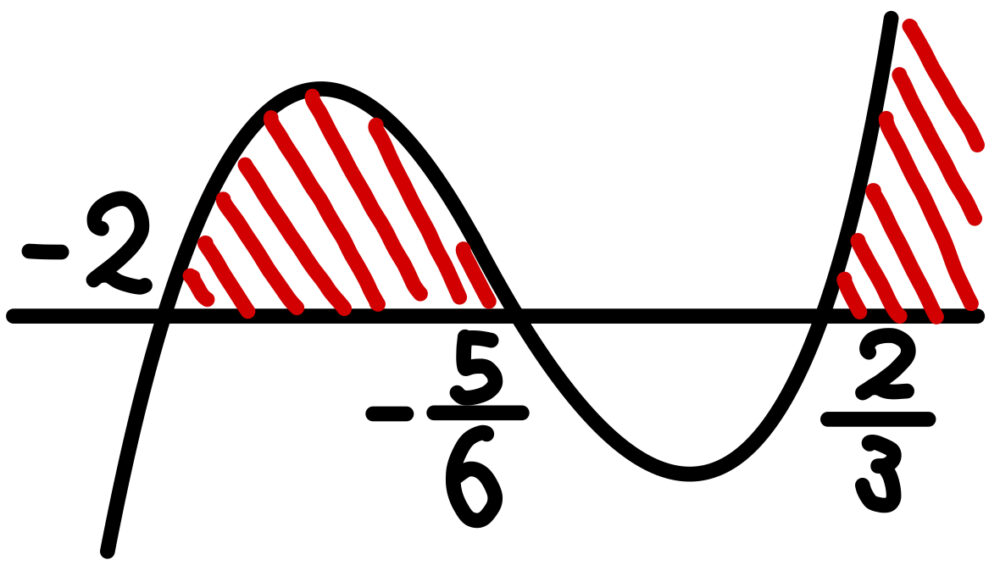 \((x+2)(6x+5)(3x-2)>0\)
\((x+2)(6x+5)(3x-2)>0\)
よって,
\(-2<x<-\displaystyle\frac{5}{6}\) または \(\displaystyle\frac{2}{3}<x\)
(2) 恒等式
\(6x^2+17x+10=(3x-2)(2x+7)+24\) より
\(f(x)=\displaystyle\frac{(3x-2)(2x+7)+24}{3x-2}=2x+7+\displaystyle\frac{24}{3x-2}\)
したがって,\(f(x)=Ax+B+\displaystyle\frac{C}{3x-2}\) が \(x\) についての恒等式となるのは,
\(A=2\),\(B=7\),\(C=24\)
(3) \(f(n)\) が正の整数とな整数 \(n\)
(1)の結果から
\(f(n)>0\) \(\iff\) \(-2<n<-\displaystyle\frac{5}{6}\) または \(\displaystyle\frac{2}{3}<n\)
つまり \(n\) は \(-1\) または 正の整数
ここで \(f(-1)=\displaystyle\frac{1}{5}\) より \(f(n)\) は整数とならないため \(n=-1\) は不適.
また,(2)の結果より
\(f(n)=2n+7+\displaystyle\frac{24}{3n-2}\)
\(n>0\) より \(3n-2>0\)なので
\(f(n)\) が正の整数となるのは,\(3n-2\) が \(24\) の正の約数となるとき.
よって,\(3n-2=1,2,3,4,6,8,12,24\)
ここで,\(3n-2\) は \(3\) で割ると \(1\) 余る整数であるから,
\(3n-2=1,4\)
したがって,\(n=1,2\)







コメント