【2023上智大学・経済・第1問(4)】
平方数とは自然数の \(2\) 乗で表される数である.\(1\),\(4\),\(9\),\(16\),\(\cdots\) は平方数である.
\(x\) を自然数とする.\(x\) 以下の平方数のうち \(5\) で割ると余りが \(j\) となるものの個数を \(N(x,j)\) と表す.例えば,\(N(10,0)=0\),\(N(10,1)=1\),\(N(10,2)=0\),\(N(10,3)=0\),\(N(10,4)=2\) である.
( ⅰ ) \(N(1000,0)=\) [ エ ] ,\(N(1000,2)=\) [ オ ] である.
( ⅱ ) \(N(x,1)=3\) を満たす最大の \(x\) は [ カ ] である.
平方数・指数は合同式が有効
平方数と合同式は非常に相性抜群です!特に \(mod 3\) や \(mod 4\) は頻出です!
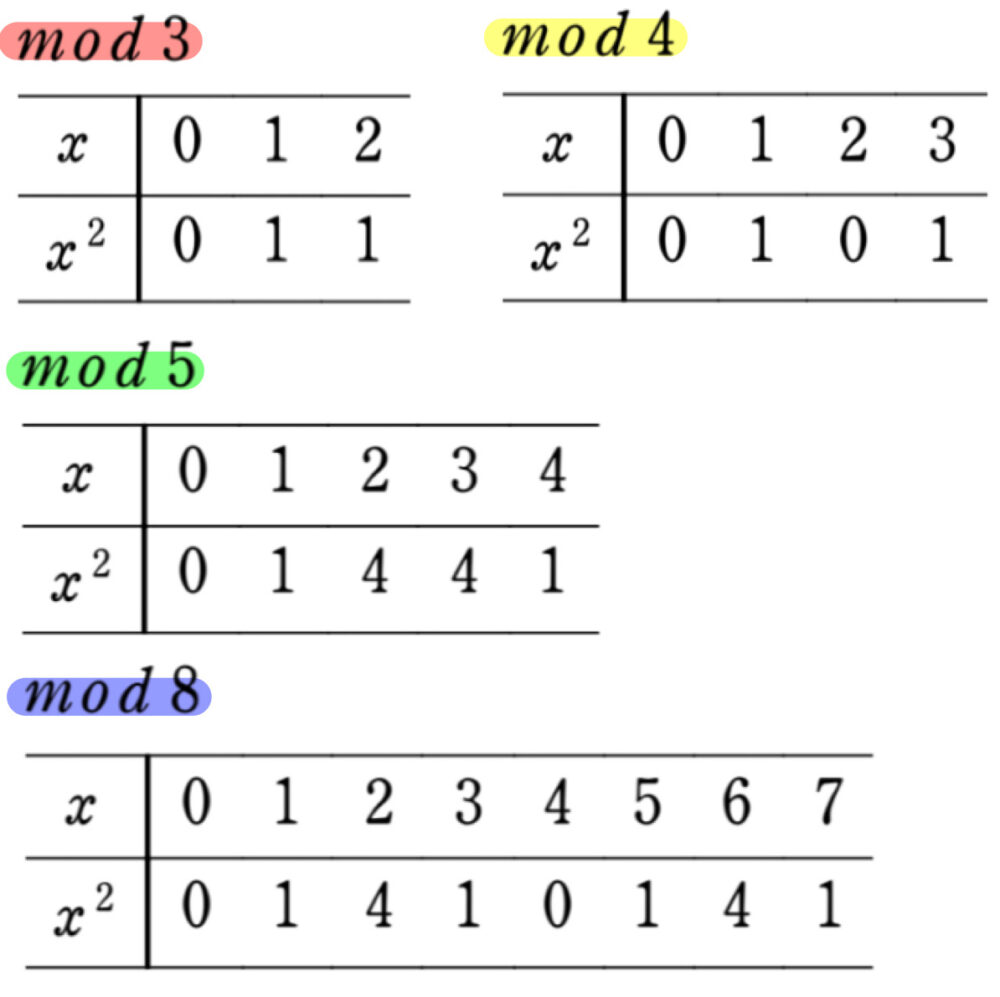
- mod 3 ➡ 「0、1」のみ
- mod 4 ➡ 「0、1」のみ
- mod 5 ➡ 「0、1、4」のみ
- mod 8 ➡ 「0、1、4」のみ

解答・解説
( ⅰ ) 以下,\(mod5\) として考える.
\(n\) を自然数とすると,
\(n≡0,\pm 1,\pm 2\) のとき \(n^2≡0,1,4\) ・・・①
\(N(1000,0)\) を満たすのは
\(5^2,10^2,15^2,20^2,25^2,30^2\) の \(6\) 個
\(N(1000,0)=6\) ・・・[ エ ]
①より \(N(1000,2)\) は存在しないため
\(N(1000,2)=0\) ・・・[ オ ]
( ⅱ )
①より,\(n^2≡1\) \(\iff\) \(n≡\pm 1\) ( \(mod5\) ) なので,
\(5\) で割った余りが \(1\) となる平方数は小さい順に
\(1^2,4^2,6^2,9^2,\cdots\) となる.
よって,\(N(x,1)=3\) を満たす最大の \(x\) は \(9^2-1=\) \(80\) ・・・[ カ ]







コメント