【問題12】
複素数平面上で \(| iz+3 |≦1\) を満たす \(z\) に対して、
\(| z-i+2 |\) の最大値と最小値を求めよ.
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
\(| z – \alpha |≦r\) について
☆\(| \beta – \alpha|\) は \(2\) 点 \(\alpha\)、\(\beta\) の距離
であるから、\(| z – \alpha |=r\) は、\(2\) 点 \(z\) と \(\alpha\) の距離が常に \(r\) になることを表す.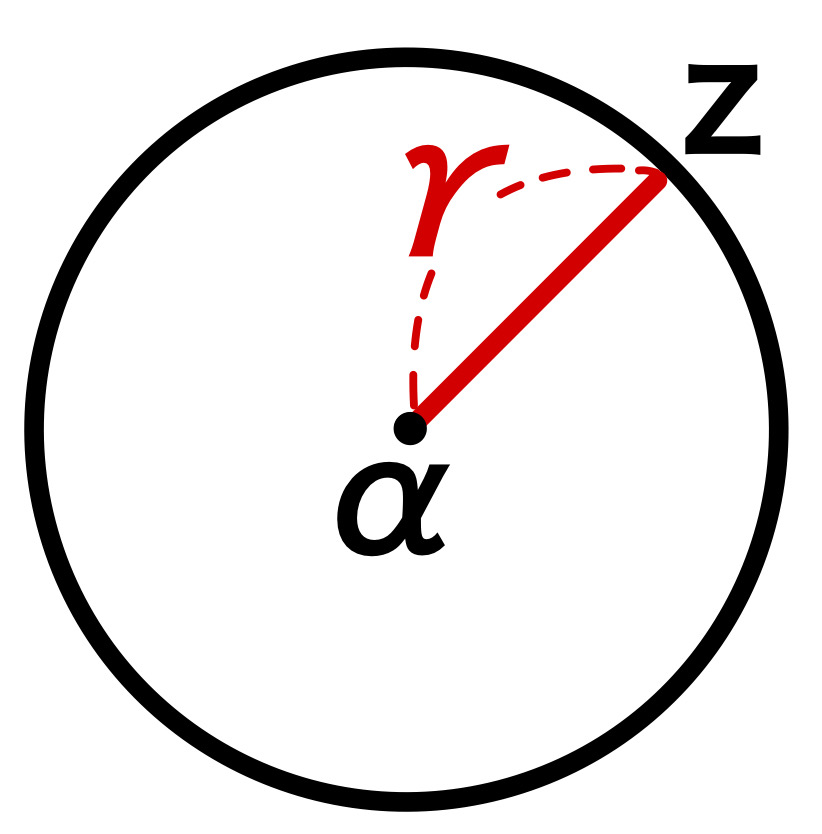
つまり点 \(z\) が表す軌跡は、中心 \(\alpha\) 、半径 \(r\) の円.
このことから、
\(| z – \alpha |≦r\) ・・・中心 \(\alpha\) 、半径 \(r\) の円の内部(円周上を含む)
\(| z – \alpha |>r\) ・・・中心 \(\alpha\) 、半径 \(r\) の円の外部(円周上は含まない)
と言うことが分かる.
解答
\(| iz+3 |≦1\) \(\iff| i || z-3i |≦1\)
\(| i |=1\) より、\(| z-3i |≦1\)
よって、中心 \(3i\)、半径 \(1\) の円周および内部を表す.
ここで、\(| z-i+2 |=k\) とおく.
これは、中心 \(i-2\)、半径 \(k\) の円を表すので、
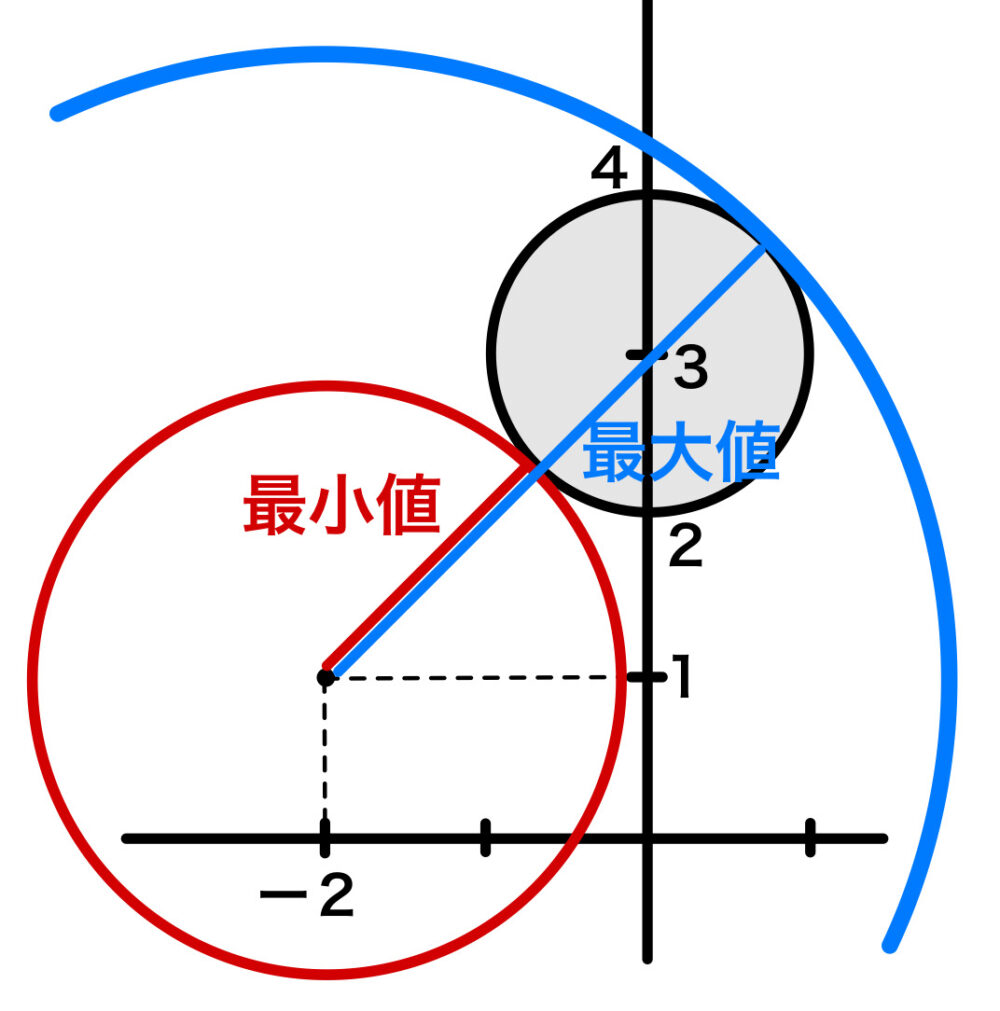
\(| z-i+2 |\) が最小となるのは、
\(2\) 円が上図のように外接するときで、最小値 \(2\sqrt{2}-1\)
\(| z-i+2 |\) が最大となるのは、
\(2\) 円が上図のように内接するときで、最大値 \(2\sqrt{2}+1\)

https://mathmathmanabu.com/cos2π-7/






コメント