【1994 名古屋大学】
長方形内に置かれた三角形の面積は、もとの長方形の面積の \(\displaystyle\frac{1}{2}\) を超えないことを示せ.
はじめに
平面図形問題は、方針に気がつけるかどうかで「満点」か「0点」か非常に差がつきやすい分野です.
ここでの最大の目的は、「0点」を阻止すること!
「満点」は無理でも、少しでも部分点をとり、最悪のケースを免れるためのポイントとしてお話をしていきます.
平面図形の問題は、勝手に分野を決めつけるな!
平面図形の問題で、一番やってはいけないことは、勝手に分野を決めつけてしまうことです.
共通テストのように、分野が決まっている場合は良いのですが、2次試験の問題においては、どの分野の融合問題であるかは、見た目だけでは分かりません.
Point:平面図形
パターン問題を除き、次の原則3つを考える
1.幾何
2.座標
3.ベクトル
※数学Ⅲまで学習している人は、
4.複素数平面
5.極座標 などもあります!
基本的な問題で、上のPointについてで紹介しています.
【差がつく考え方】平面図形の3つのアプローチ!(幾何・座標・ベクトル)
ご参考に!
考え方
方針がつかめない平面図形の問題に出会った場合、私が考えることは、Pointの1~3を順番(別に順番はどれからでもOK)に考えていきます.
1.幾何について
ここで言う幾何とは、三角比(正弦定理や余弦定理など)、円周角の定理、相似や合同など、THE図形として考えてみます.
例えば長方形の各辺の長さ、三角形の各辺、角度を何か文字でおいて・・・.
相似や合同な図形はないか・・・などなど
それでどこまで解答が書けそうか試してみます.
※全く点数がもらえそうな記述ができなければ、撤退!次を考える!
2.座標について
\(x\)、\(y\) 軸をとり、各点に座標を設定します.
※直角があると、原点に取りやすい!
※今回は座標で解答を作成します.詳細は後程
文字が多くなり、計算は非常に大変になる傾向がありますが、最悪ゴリ押しで答えを導けることが多いです.
※座標の設定は工夫しましょう!工夫次第で、後々の計算量が大きく変わります.
3.ベクトルについて
非常に汎用性が広い解法になります.また平面だけでなく、空間の問題もベクトルの世界に引きずり込むことで、今一正確な図形が把握できなくても、ベクトルの計算でどうにかできる頼れるアイテム!
もちろん1~3のどれかだけで解くと言うことを言っているわけではありません.
1~3をやってみて、使えそうなパーツをそれぞれから掻い摘んで「0点」を阻止すると言うのが大切です.
結果的に解けた解けなかったは良いとして、普段の練習から常に3パターンを考える癖を身に付けましょう.練習でできないことは、入試本番では絶対にできません.![]()
解答(座標の利用)
【1994 名古屋大学】
長方形内に置かれた三角形の面積は、もとの長方形の面積の \(\displaystyle\frac{1}{2}\) を超えないことを示せ.
図のように、\(O\) を原点、\(A ( a , 0 )\)、\(B ( 0 , b )\)、\(C ( a , b )\) をとり、四角形 \(OACB\) を考える.
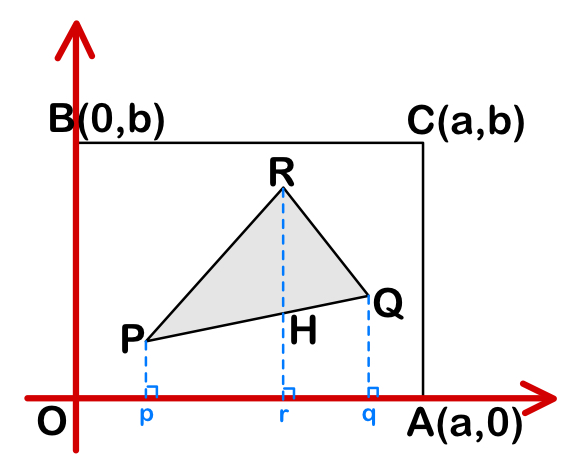
さらに、四角形 \(OACB\) の内部(境界線上を含む)に、\( \triangle PQR\) をとり、\(P\)、\(Q\)、\(R\) の \(x\) 座標をそれぞれ \(p\)、\(q\)、\(r\) とおく.
また、\(x=r\) と 直線 \(PQ\) の交点を \(H\) とする.
ただし、\(a\)、\(b\) は正の定数で、\(p\)、\(q\)、\(r\) は \(0≦p≦q≦r≦a\) を満たすとする.
このとき、四角形 \(OACB = ab\) ・・・①
\( \triangle PQR = \triangle PRH + \triangle QRH \) より
\( \triangle PQR = \displaystyle\frac{1}{2}\cdot RH\cdot (r-p) + \displaystyle\frac{1}{2}\cdot RH\cdot (q-r)\\ = \displaystyle\frac{1}{2}\cdot RH\cdot \left\{(r-p)+(q-r)\right\}\\=\displaystyle\frac{1}{2}\cdot RH\cdot (q-p)\) ・・・②
\(RH≦OB=b\)、\(q-p≦OA=a\) より
\( RH\cdot (q-p)≦ab\) ・・・③
①、②、③より
\( \triangle PQR ≦ \displaystyle\frac{1}{2} ab\)![]()







コメント