完全順列(モンモール数)とは
※攪乱(かくらん)順列ともいう
つまり、プレゼント交換をする際に、「自分が準備したプレゼントが、自分に返ってこない」ようにするために考えた場合の数です。
とても有名な順列で、2022年の共通テストで出題されまた。
また、2次試験においても定期的に様々な大学で出題されていますので、これを機に理解を!
問題と解説

まず初めに、説明のために
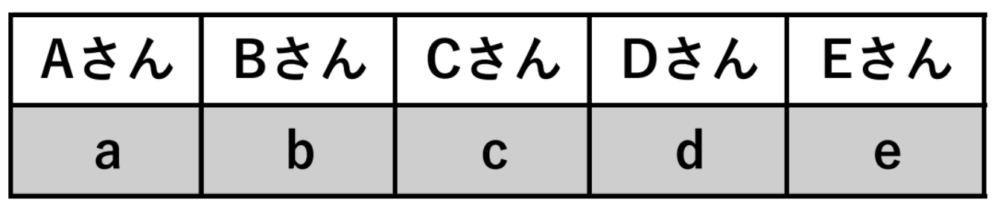
\(A\) さんが準備したプレゼントを \(a\)、
\(B\) さんが準備したプレゼントを \(b\)、
\(C\) さんが準備したプレゼントを \(c\)、
\(D\) さんが準備したプレゼントを \(d\)、
\(E\) さんが準備したプレゼントを \(e\) と呼ぶことにします。
(1)問題・解答・解説 《ア ~コ》

(1) の ( ⅰ )《ア〜コ》
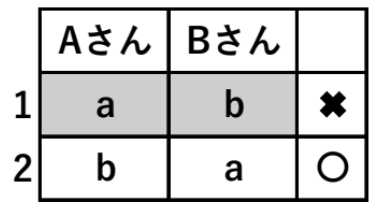
1回の交換で終了する(全員が自分以外の持参したプレゼントを受け取る)のは、上の表から
\(1\) 通り ・・・《ア》
また確率は、\(\displaystyle\frac{1}{2}\) ・・・《イウ》
(1) の ( ⅱ )《エ~カ》

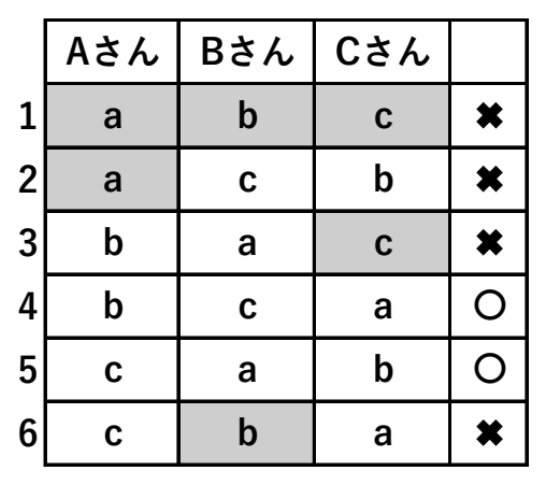
1回の交換で終了する(全員が自分以外の持参したプレゼントを受け取る)のは、上の表から
\(2\) 通り ・・・《エ》
また確率は、\(\displaystyle\frac{2}{3!}=\displaystyle\frac{1}{3}\) ・・・《オ,カ》
(1) の (ⅲ)《キ~コ》

1回で終了、2回で終了、3回で終了、4回で終了のときと場合分けをしてもよいが大変!
☞ 余事象の利用!
全事象から、「4回までに終了しない」を除けばよい
(1) の (ⅱ) より、1回で終了する確率は \(\displaystyle\frac{1}{3}\) であったので、
1回で終了しない確率は、\(1-\displaystyle\frac{1}{3}=\displaystyle\frac{2}{3}\)
したがって求める確率は、\(1-\left(\displaystyle\frac{2}{3}\right)^4=\)\(\displaystyle\frac{65}{81}\) ・・・《キ~コ》![]()
![]()
(2)問題・解答・解説《サ~タ》
 (1)でやったように、\(4!=24\) 通りをすべて書いて、〇 or ✖ と調べても良い!
(1)でやったように、\(4!=24\) 通りをすべて書いて、〇 or ✖ と調べても良い!
しかし、\(5!=120\) 通りとなるとなかなか大変である。(もちろん時間に余裕があればやっても良いが、共通テストではそんなに時間は・・・)
そこで、誘導がにのって解答を考えてみます。
(2)《サ》について
4人のうち、ちょうど1人が自分の持参したプレゼントになる場合、
まず初めに誰がその1人になるか・・・\({}_4 C_1=4\) 通り
以下では仮に \(A\) さんが \(a\) のプレゼントを受け取った場合を考えます。
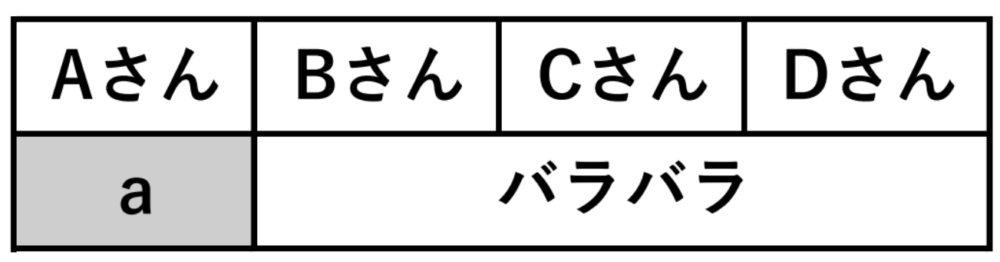
残りの3人がバラバラになるようにプレゼント交換が出来ればよいので、これは(1) の (ⅱ) の[エ]と同じである。つまり、\(2\) 通り
よって、\(4\times 2=\)\(8\) 通り ・・・《サ》
(2)《シ》について
4人のうち、ちょうど2人が自分の持参したプレゼントになる場合、
まず初めに誰がその2人になるか・・・\({}_4 C_2=6\) 通り
以下では仮に \(A\)、\(B\) さんが自分のプレゼントを受け取った場合を考えます。
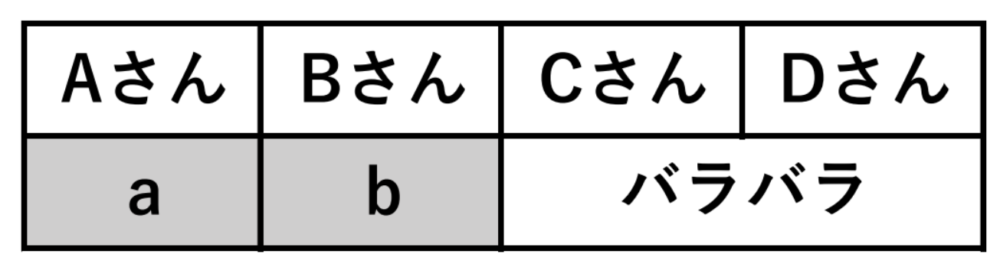
残りの2人がバラバラになるようにプレゼント交換が出来ればよいので、これは(1) の (ⅰ) の[ア]と同じである。つまり、\(1\) 通り
よって、\(6\times 1=\)\(6\) 通り ・・・《シ》
(2)《ス~タ》について
上で求めた、[サ]と[シ]と、全員が自分のプレゼントをもらう \(1\) 通り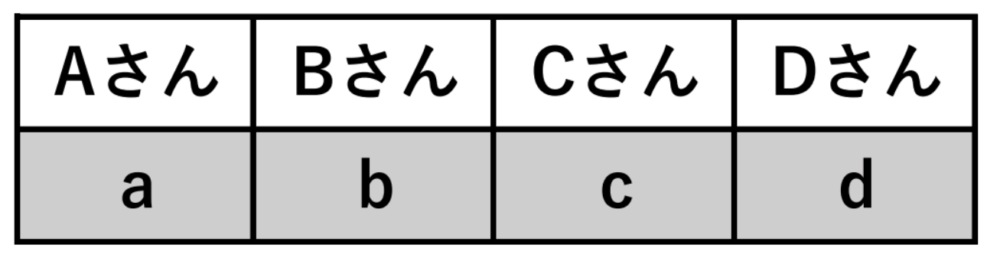
を考えて、\(8+6+1=\)\(15\) 通り ・・・《ス、セ》
したがって、4人で1回目の交換で終了するのは \(4!-15=9\) 通りであるから、求める確率は、
\(\displaystyle\frac{9}{4!}=\)\(\displaystyle\frac{3}{8}\) ・・・《ソ、タ》
(3)問題・解答・解説《チ~ト》

4人の場合と同様に考えていく
① 5人中1人が自分のプレゼントのとき
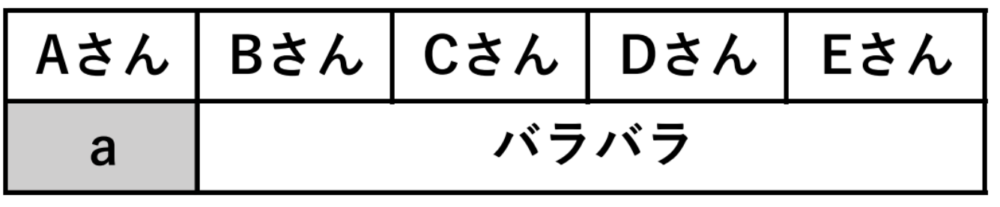
\({}_5 C_1\times 9=45\) 通り
② 5人中2人が自分のプレゼントのとき
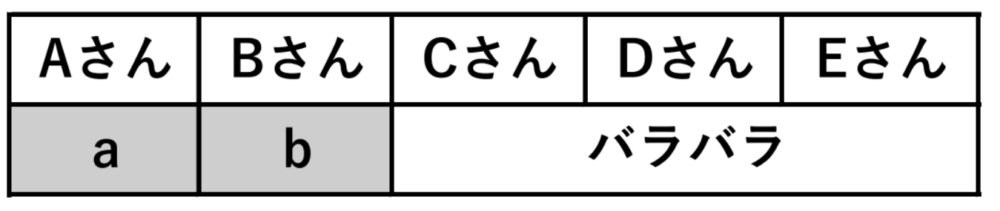
\({}_5 C_2\times 2=20\) 通り
③ 5人中3人が自分のプレゼントのとき
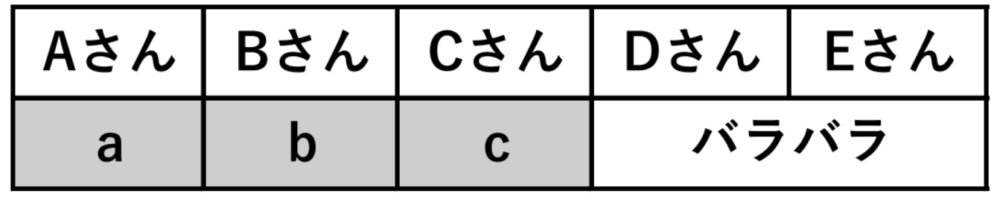
\({}_5 C_3\times 1=5\) 通り
④ 全員が自分のプレゼントのとき
\(1\) 通り
①~④より、5人で1回交換をして、終了しないのは \(45+20+10+1=76\) 通りであるから、
5人で1回交換をして、終了するのは \(5!-76=44\) 通り
したがって求める確率は、\(\displaystyle\frac{44}{5!}=\)\(\displaystyle\frac{11}{30}\) ・・・《チ~ト》
(4)問題・解答・解説《ナ~ネ》
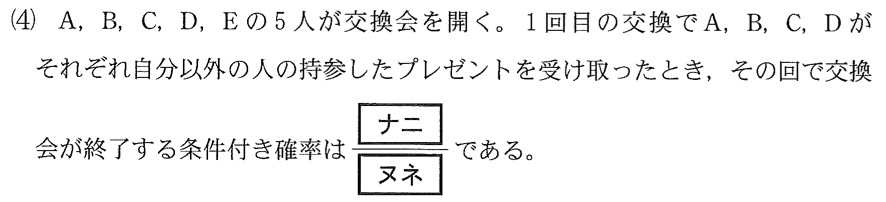
\(A\)、\(B\)、\(C\)、\(D\) がそれぞれ自分以外の人のプレゼントを受け取るのは、
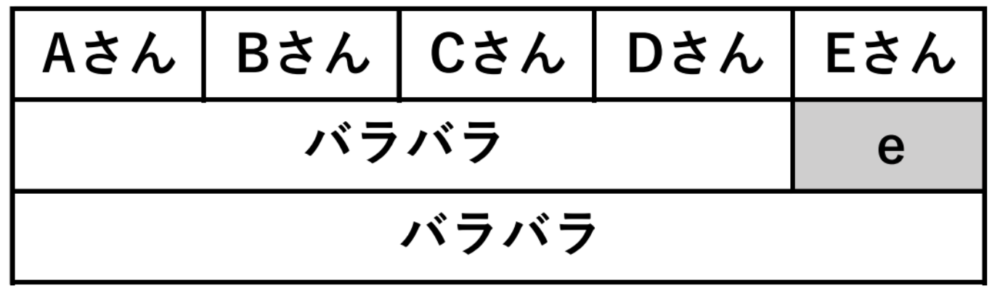
(Ⅰ) \(E\) さんが \(e\) を受け取る場合
(Ⅱ) \(E\) さんが \(e\) を受け取らない(5人ともバラバラ)
の2つの場合が考えられる.
(Ⅰ)は4人がバラバラになる場合であるから、\(9\) 通り
(Ⅱ)は5人がバラバラになる場合であるから、\(44\) 通り
したがって求める条件付き確率は、
\(\displaystyle\frac{44}{44+9}=\)\(\displaystyle\frac{44}{53}\) ・・・《ナ~ネ》
参考(一般化)
となることが分かっています。
説明は長くなる&少し難しいのでここでは省略しますが、とりあえず有名な問題ですので結果だけでも知っておいて損はないかと。
ちなみに、「\(a_{n}=(n-1)(a_{n-1}+a_{n-2})\)」については、この関係式を導く問題が2次試験でもよく見かけます。
ご参考までに結論は知っておきましょう!
また確率で有名問題として、「確率の最大」があります。
2次試験でも頻出テーマになりますので、

を参考に、考え方を学びましょう!









コメント