【2021数学ⅠA(第2日程)】第２問[２](２次関数)

(１)問題と解答・解説《キ〜コ》

放物線 \(C_{1}\) は \(P_{0}(0,3)\)，\(M(4,3)\) を通るので，

頂点の \(x\) 座標は \(x=2\) とわかる．

よって，\(y=a(x-2)^2+b\) の形で表せるので，

\(y=ax^2-4ax+4a+b\)

これが \(P_{0}(0,3)\) を通るので，\(4a+b=3\)

したがって，\(y=ax^2-4ax+3\) ・・・《キク》

\(y=a(x-2)^2-4a+3\) より

「シュートの高さ」つまり \(C_{1}\) の頂点の \(y\) 座標は

\(-4a+3\) ・・・《ケコ》

\(C_{2}\)：\(y=p\left\{x-\left(2-\displaystyle\frac{1}{8p}\right)\right\}^2-\displaystyle\frac{(16p-1)^2}{64p}+2\) より

花子さんの「ボールが最も高くなるときの地上の位置」(頂点の \(x\) 座標) は

\(x=2-\displaystyle\frac{1}{8p}\) であり，

プロ選手の「ボールが最も高くなるときの地上の位置」(頂点の \(x\) 座標) は \(x=2\)

ここで，\(C_{2}\) は上に凸の放物線であるから，\(p<0\) となるので，

\(2-\displaystyle\frac{1}{8p}>2\)

したがって，《サ：②》

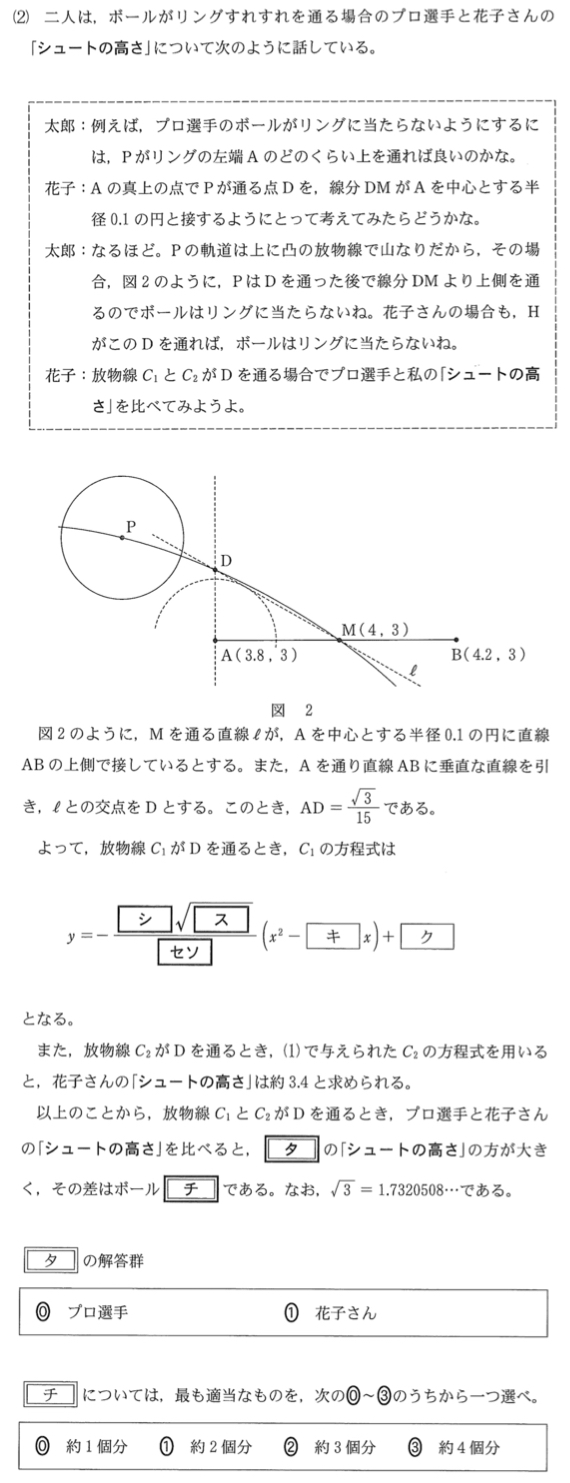
\(AD=\displaystyle\frac{\sqrt{3}}{15}\) より \(D\left(3.8,3+\displaystyle\frac{\sqrt{3}}{15}\right)\)

\(C_{1}\) が \(D\) を通るとき

\(3+\displaystyle\frac{\sqrt{3}}{15}=a(3.8-2)^2-4a+3\)

\(\iff\) \(a=-\displaystyle\frac{5\sqrt{3}}{57}\)

よって，\(y=-\displaystyle\frac{5\sqrt{3}}{57}\left(x^2-4x\right)+3\) ・・・《シ〜ソ》

プロ選手のシュートの高さ(\(C_{1}\) の頂点の \(y\) 座標)は

\(-4a+3=-4\times \left(-\displaystyle\frac{5\sqrt{3}}{57}\right)+3=\displaystyle\frac{20\sqrt{3}}{57}+3\)

\(\sqrt{3}≒1.7\) として考えると，

\(\displaystyle\frac{20\sqrt{3}}{57}≒\displaystyle\frac{34}{57}≒0.6\)

よってプロ選手のシュートの高さは約 \(3.6 m\) となる．

したがって，《タ：⓪プロ選手》の「シュートの高さ」の方が大きく，

その差は，約 \(3.6-3.4=0.2 m\) より，ボール《チ：⓪約 \(1\) 個分》