【2020 大阪大学・文系[第2問]】
円周を \(3\) 等分する点を時計回りに \(A\)、\(B\)、\(C\) とおく.点 \(Q\) は、\(A\) から出発し、\(A\)、\(B\)、\(C\) を以下のように移動する.
\(1\) 個のさいころを投げて、\(1\) の目が出た場合は時計回りに隣の点に移動し、\(2\) の目が出た場合は反時計回りに隣の点に移動し、その他の目が出た場合は移動しない.
さいころを \(n\) 回投げたあとに \(Q\) が \(A\) に位置する確率 \(p_{n}\) とする.以下の問いに答えよ.
(1) \(p_{2}\) を求めよ.
(2) \(p_{n+1}\) を \(p_{n}\) を用いて表せ.
(3) \(p_{n}\) を求めよ.
確率漸化式と呼ばれる、数学Aの確率と、数学Bの数列(漸化式)の分野の融合問題です。
あまり学校の授業や教科書等では扱われませんが、入試においては頻出テーマになります。
様々な大学で出題されていますので、しっかりと演習をしていきましょう!
確率漸化式について
確率漸化式の問題が解けるようになるためには、大きく3つのステップがあります。
その① 確率漸化式の問題であると気がつくこと
今回の問題は、(2)で \(p_{n}\) と \(p_{n+1}\) の関係式を作れと言われているため、比較的確率漸化式だと気がつきやすい。
しかし、仮に誘導がなく、また問題文に \(p_{n}\) が登場しなかった場合、つまり
『さいころを \(n\) 回投げたあとに \(Q\) が \(\A) に位置する確率を求めよ.』
という問題のときに、この問題が確率漸化式の問題であるかどうか気が付けますか??
確率漸化式で一番の難しいのは気が付けるかどうか。特に難関大学を志望している場合、誘導が無いケールが多いです。なぜこの問題を見て確率漸化式であると気が付けるのか、その点についてもしっかりと考え方を勉強しておきましょう!
詳しい考え方、問題への着眼点については、

をご確認ください。ステップ①、②について複数の問題を使って紹介しています。
その② 式を立てること
確率漸化式の問題であると気が付けたとしましょう。
次に待ち構えるのは、立式できるかどうか。
考え方としては、
確率漸化式の立式の仕方
(ⅰ)初めの1手で場合分け
最後の1手で場合分け
\(n\) 回目と \(n+1\) 回目に注目して考える.
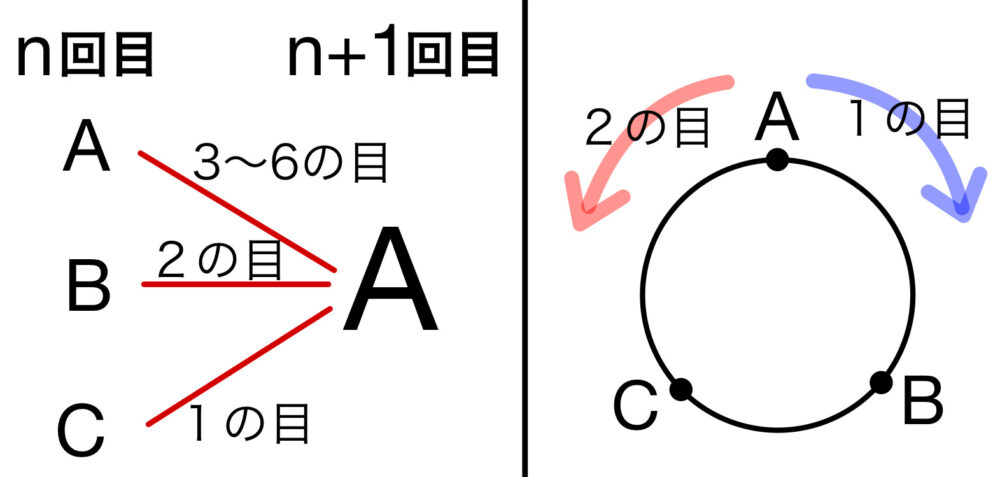
のいずれかである。
ここで、\(n\) 回目に \(A\) にいる確率は \(p_{n}\) であり、
\(n\) 回目に \(B\)、\(C\) にいる確率をそれぞれ \(q_{n}\)、\(r_{n}\) と呼ぶと、
\(n+1\) 回目に \(A\) にいる確率は \(p_{n+1}\) は、
\(p_{n+1}=\displaystyle\frac{4}{6}p_{n}+\displaystyle\frac{1}{6}q_{n}+\displaystyle\frac{1}{6}r_{n}\)
という関係式が得られる.
また、\(n\) 回目において、確率の全体が \(1\) であることを考えると、
\(p_{n}+q_{n}+r_{n}=1\) という関係が成り立つ.
その③ 漸化式が解けること
等差数列型、等比数列型、階差数列型、隣接二項間(特性方程式)・・・・・などなど、人によって分け方や名前は違いますが、漸化式の解法パターンはたくさんあります。
漸化式の解法については、もちろん理解も大切ですが、「この形を見たらこのように解く!」という完全パターンもの。
ここでは漸化式の解き方についての詳しい説明は省略しますが、丸暗記でOKですので、しっかりとまとめて覚えましょう!
解答
(1) \(p_{2}\) を求めよ.
(1) \(2\) 回さいころを投げた後、\(Q\) が \(A\) に位置するのは、
(ⅰ) \(2\) 回中、\(1\) 回は \(1\) の目、\(1\) 回は \(2\) の目
(ⅱ) \(2\) 回ともに \(3\) 以上の目
のときである.
(ⅰ) のとき \(_{2}C_{1}\times \displaystyle\frac{1}{6} \times \displaystyle\frac{1}{6}=\displaystyle\frac{1}{18}\)
(ⅱ) のとき \(\left(\displaystyle\frac{4}{6}\right)^2=\displaystyle\frac{4}{9}\)
(ⅰ)、(ⅱ)より
\(p_{2}=\displaystyle\frac{1}{18}+\displaystyle\frac{4}{9}=\displaystyle\frac{1}{2}\)
(2) \(p_{n+1}\) を \(p_{n}\) を用いて表せ.
のいずれかである。
ここで、\(n\) 回目に \(A\) にいる確率は \(p_{n}\) であり、
\(n\) 回目に \(B\)、\(C\) にいる確率をそれぞれ \(q_{n}\)、\(r_{n}\) とおくと、
\(n+1\) 回目に \(A\) にいる確率は \(p_{n+1}\) は、
\(p_{n+1}=\displaystyle\frac{4}{6}p_{n}+\displaystyle\frac{1}{6}q_{n}+\displaystyle\frac{1}{6}r_{n}\)
よって、\(p_{n+1}=\displaystyle\frac{2}{3}p_{n}+\displaystyle\frac{1}{6}(q_{n}+r_{n})\) ・・・①
という関係式が得られる.
また、\(p_{n}+q_{n}+r_{n}=1\) より
\(q_{n}+r_{n}=1-p_{n}\) であるから、①より
\(p_{n+1}=\displaystyle\frac{2}{3}p_{n}+\displaystyle\frac{1}{6}(1-p_{n})\)
したがって、\(p_{n+1}=\displaystyle\frac{1}{2}p_{n}+\displaystyle\frac{1}{6}\)
(3) \(p_{n}\) を求めよ.
隣接二項間(特性方程式)型の解き方
隣接二項間(特性方程式)型
\(a_{n+1}=pa_{n}+q\) ・・・(☆) において
\(x=px+q\) (☜特性方程式) を解いて求まる解を \(x=\alpha\) とすると、
(☆) \(\iff\) \(a_{n+1}-\alpha=p(a_{n}-\alpha)\) ( ☜等比数列型 ) に変形できる.
※特性方程式は記述で残す必要はない.
\(x=\displaystyle\frac{1}{2}x+\displaystyle\frac{1}{6}\) を解いて
\(x=\displaystyle\frac{1}{3}\)
\(p_{n+1}=\displaystyle\frac{1}{2}p_{n}+\displaystyle\frac{1}{6}\)
\(\iff\) \(p_{n+1}-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{2}\left(p_{n}-\displaystyle\frac{1}{3}\right)\) より、
数列 \(\left\{p_{n}-\displaystyle\frac{1}{3}\right\}\) は公比 \(\displaystyle\frac{1}{2}\) の等比数列であるから、
\(p_{n}-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{2}\left(p_{1}-\displaystyle\frac{1}{3}\right)\)
ここで、\(p_{1}=\displaystyle\frac{2}{3}\) であるから、
\(p_{n}-\displaystyle\frac{1}{3}=\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^{n-1}\)
以上より、\(p_{n}=\displaystyle\frac{1}{3}\left(\displaystyle\frac{1}{2}\right)^{n-1}+\displaystyle\frac{1}{3}\)
おまけ:数Ⅲを学習した人へ
(3)で求めた \(p_{n}\) に対して、\(n\rightarrow\infty\) を考えると、
\(n\rightarrow\infty\) のとき \(\left(\displaystyle\frac{1}{2}\right)^{n-1}\rightarrow 0\) であるから、
\(p_{n}\) は \(\displaystyle\frac{1}{3}\) に収束することが分かる.
これは当たり前なのは分かるだろうか?
\(n\) の回数を限りなく大きくすると、点 \(Q\) は \(A\) または \(B\) または \(C\) に等確率にいると言うことである。
このような当たり前のことを当たり前に思えるかどうかが非常に大切で、仮に自分の求めた答えの極限を考えた際に、\(\displaystyle\frac{1}{3}\) でなければ明らかにどこかで間違えていることが分かる。
もちろん計算ミスをしないのが理想であるが、本当に大切なのは、ミスに気が付けること。
些細なことかもしれないが、このようなことは大切にしていって欲しい。
確率漸化式の演習
他にも様々なタイプの確率漸化式の問題をまとめています。
立式の演習にご活用ください。








コメント