【2023数学ⅡB(第1日程)】第2問[1](微分法)
[1](1)問題と解答・解説《ア〜ク》

[1](1)解答・解説《ア〜ク》
\(k\) を正の定数とし,\(f(x)=x^2(k-x)\)
\(y=f(x)\) と \(x\) 軸との共有点の座標は,
\(f(x)=0\) \(\iff\) \(x^2(k-x)=0\)
より \(x=0,k\)
よって,\((0,0)\),\((k,0)\) ・・・《ア:④》
また,\(f(x)=-x^3+kx^2\) より
\(f^{\prime}(x)=-3x^2+2kx\) ・・・《イ〜エ》
\(f^{\prime}(x)=-x(3x-2k)\)
\(f^{\prime}(x)=0\) のとき \(x=0,\displaystyle\frac{2k}{3}\)
\(k>0\) より増減表は
| \(x\) | ・・・ | \(0\) | ・・・ | \(\displaystyle\frac{2k}{3}\) | ・・・ |
| \(f^{\prime}(x)\) | ー | \(0\) | + | \(0\) | ー |
| \(f(x)\) | ↘️ | ↗️ | ↘️ |
\(x=0\) のとき,\(f(x)\) は極小値 \(0\) ・・・《オ:⓪,カ:⓪》
\(x=\displaystyle\frac{2k}{3}\) のとき,\(f(x)\) は極大値 \(\displaystyle\frac{4k^3}{27}\) ・・・《キ:③,ク:⑨》
(2)問題と解答・解説《ケ〜ソ》
(2)解答・解説《ケ〜ソ》
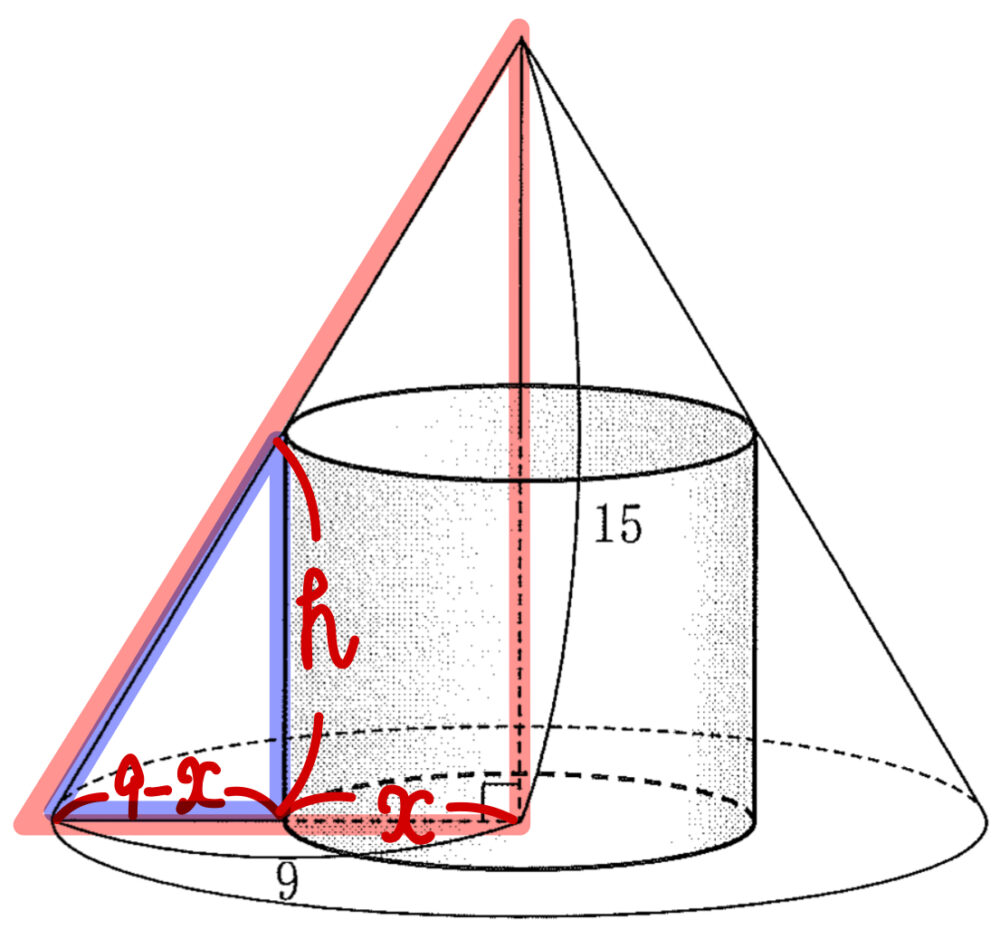 円柱の底面の半径を \(x\),高さを \(h\) とおく
円柱の底面の半径を \(x\),高さを \(h\) とおく
右図の青と赤の相似な直角三角形に注目すると
\(9-x:h=9:15\) \(\iff\) \(h=\displaystyle\frac{5}{3}(9-x)\)
よって円柱の体積 \(V\) は
\(V=x^2\pi\cdot h=\displaystyle\frac{5}{3}\pi x^2(9-x)\) ・・・《ケ〜サ》
(1)において,\(k=9\) として考えると
\(V=\displaystyle\frac{5}{3}\pi f(x)\) より
\(0<x<9\) のとき
\(x=\displaystyle\frac{2k}{3}=6\) のとき・・・《シ》
\(V\) は最大値 \(180\pi\) ・・・《ス〜ソ》







コメント