【2023数学ⅡB(第1日程)】第２問[2](積分法)

[２](１)問題と解答・解説《タ〜ネ》

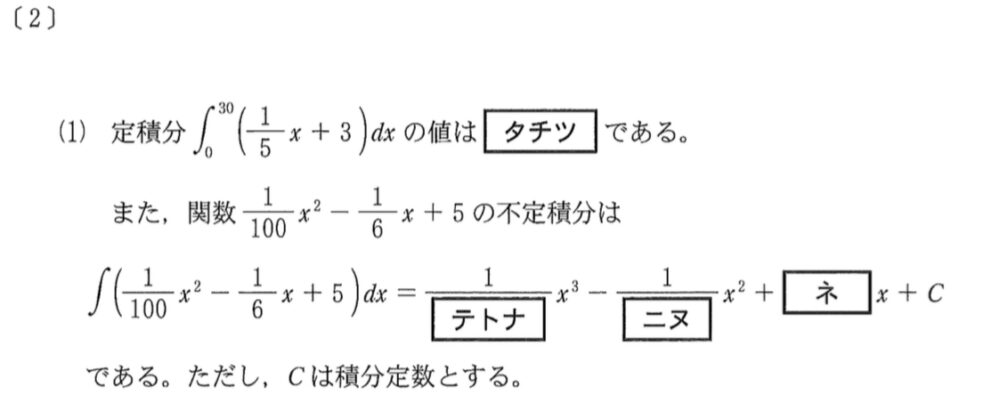
［２］(１)解答・解説《タ〜ネ》

\(\displaystyle\int^{30}_{0}\left(\displaystyle\frac{1}{5}x+3\right)dx\)

\(=\Bigl[\displaystyle\frac{1}{10}x^2+3x\Bigr]^{30}_{0}\)

\(=\)\(180\) ・・・《タ〜ツ》

また，

\(\displaystyle\int\left(\displaystyle\frac{1}{100}x^2-\displaystyle\frac{1}{6}x+5\right)dx\)

\(=\displaystyle\frac{1}{300}x^3-\displaystyle\frac{1}{12}x^2+5x+C\) ・・・《テ〜ネ》

ただし \(C\) は積分定数とする．

(２)( ⅰ )問題と解答・解説《ノ》

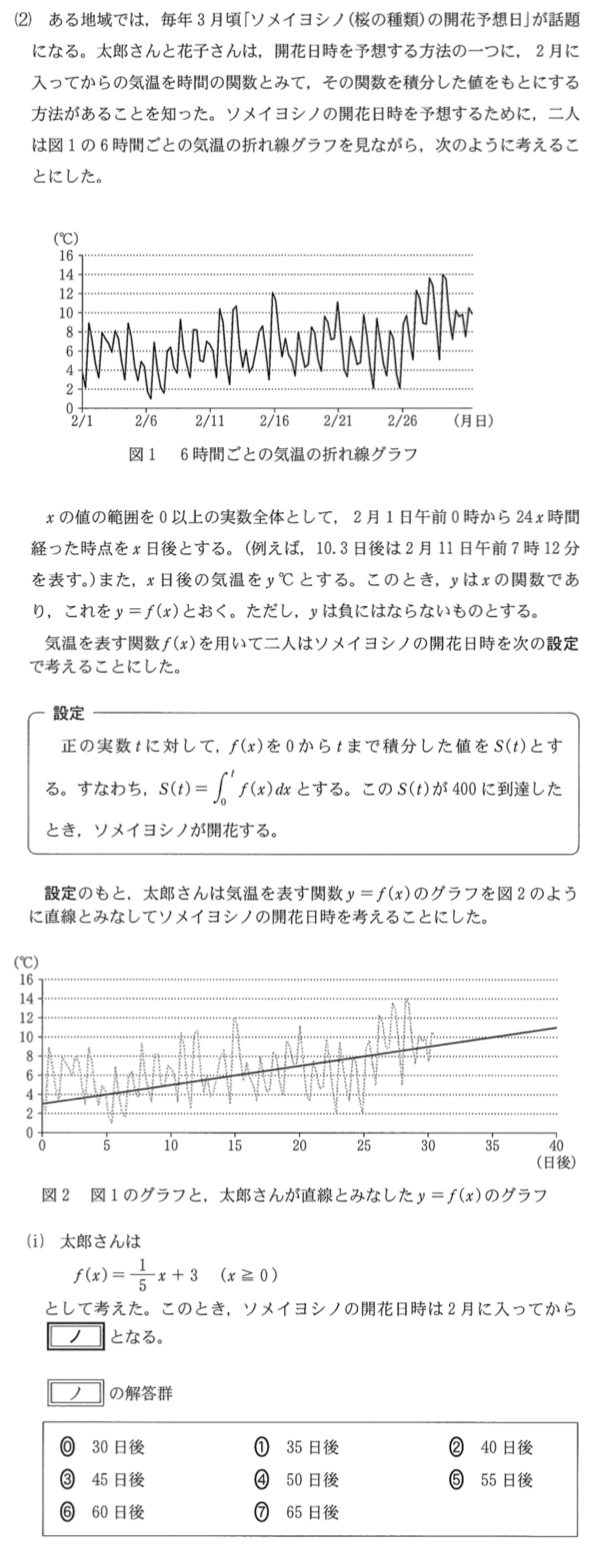
(２)( ⅰ )解答・解説《ノ》

文章が長い・・・

要約すると，\(t\) 日後までの \(f(x)\) の面積が，\(400\) を超えたら開花ということです！

ソメイヨシノの開花日時は \(2\) 月に入ってから \(t\) 日後とすると

\(\displaystyle\int^{t}_{0}\left(\displaystyle\frac{1}{5}x+3\right)dx≧400\)

\(\Bigl[\displaystyle\frac{1}{10}x^2+3x\Bigr]^{t}_{0}≧400\)

\(\displaystyle\frac{1}{10}t^2+3t≧400\)

\((t+80)(t-50)≧0\)

\(t≧0\) より，\(t≧50\)

よって，《ノ：④ \(50\) 日後》

(２)( ⅱ )問題と解答・解説《ハヒ》

(２)( ⅱ )解答・解説《ハヒ》

\(\displaystyle\int^{30}_{0}\left(\displaystyle\frac{1}{5}x+3\right)dx=180\)

\(\displaystyle\int^{40}_{30}\left(\displaystyle\frac{1}{100}x^2-\displaystyle\frac{1}{6}x+5\right)dx=115\) より

\(40\) 日後までに

\(180+115=295<400\) なので，まだ開花していない．

\(x≧30\) において \(f(x)\) は増加関数であるから，

\(\displaystyle\int^{40}_{30}\left(\displaystyle\frac{1}{100}x^2-\displaystyle\frac{1}{6}x+5\right)dx\) \(<\) \(\displaystyle\int^{50}_{40}\left(\displaystyle\frac{1}{100}x^2-\displaystyle\frac{1}{6}x+5\right)dx\) ・・・《ハ：⓪》

よって，\(\displaystyle\int^{50}_{40}\left(\displaystyle\frac{1}{100}x^2-\displaystyle\frac{1}{6}x+5\right)dx>115\) より

\(295+\displaystyle\int^{50}_{40}\left(\displaystyle\frac{1}{100}x^2-\displaystyle\frac{1}{6}x+5\right)dx>295+115=410>400\) となることがわかる．

以上より，ソメイヨシノの開花日時は \(2\) 月に入ってから

《ヒ：④ \(40\) 日後より後，かつ \(50\) 日後より前》