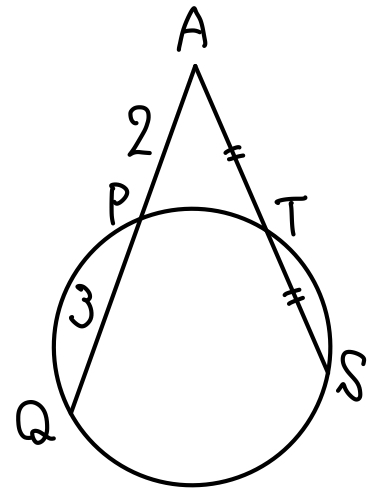
(１)問題《ア～オ》
(１)解答・解説《ア～オ》
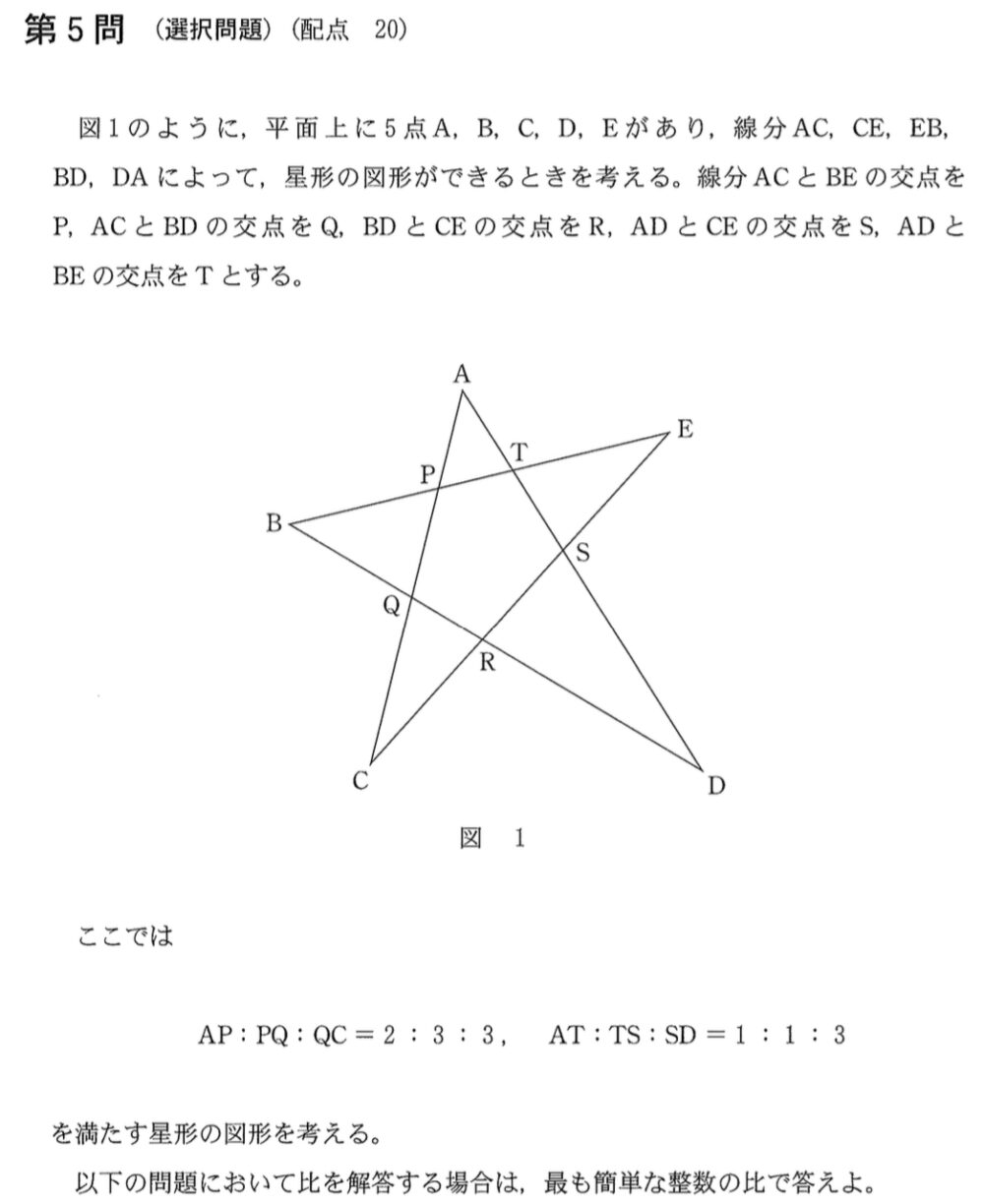
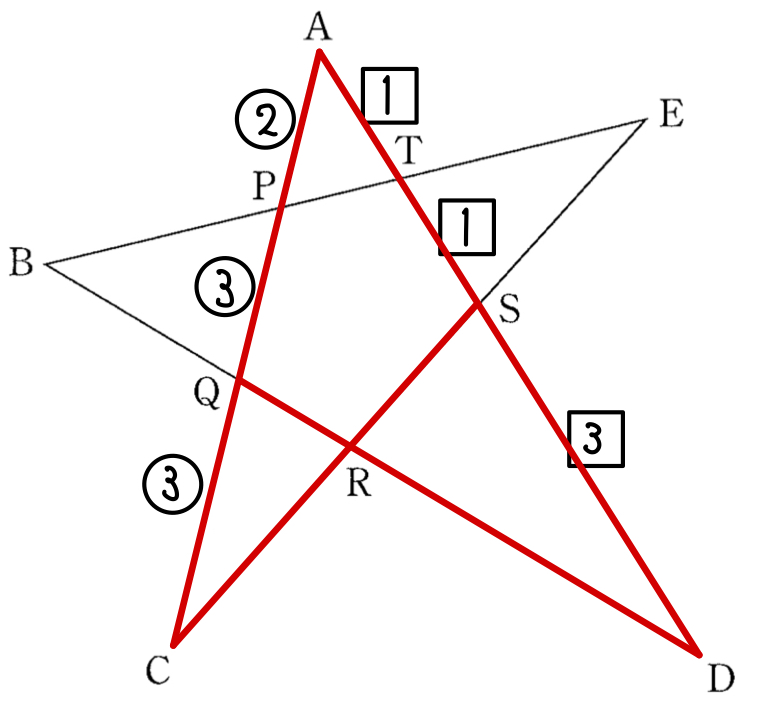メネラウスの定理より
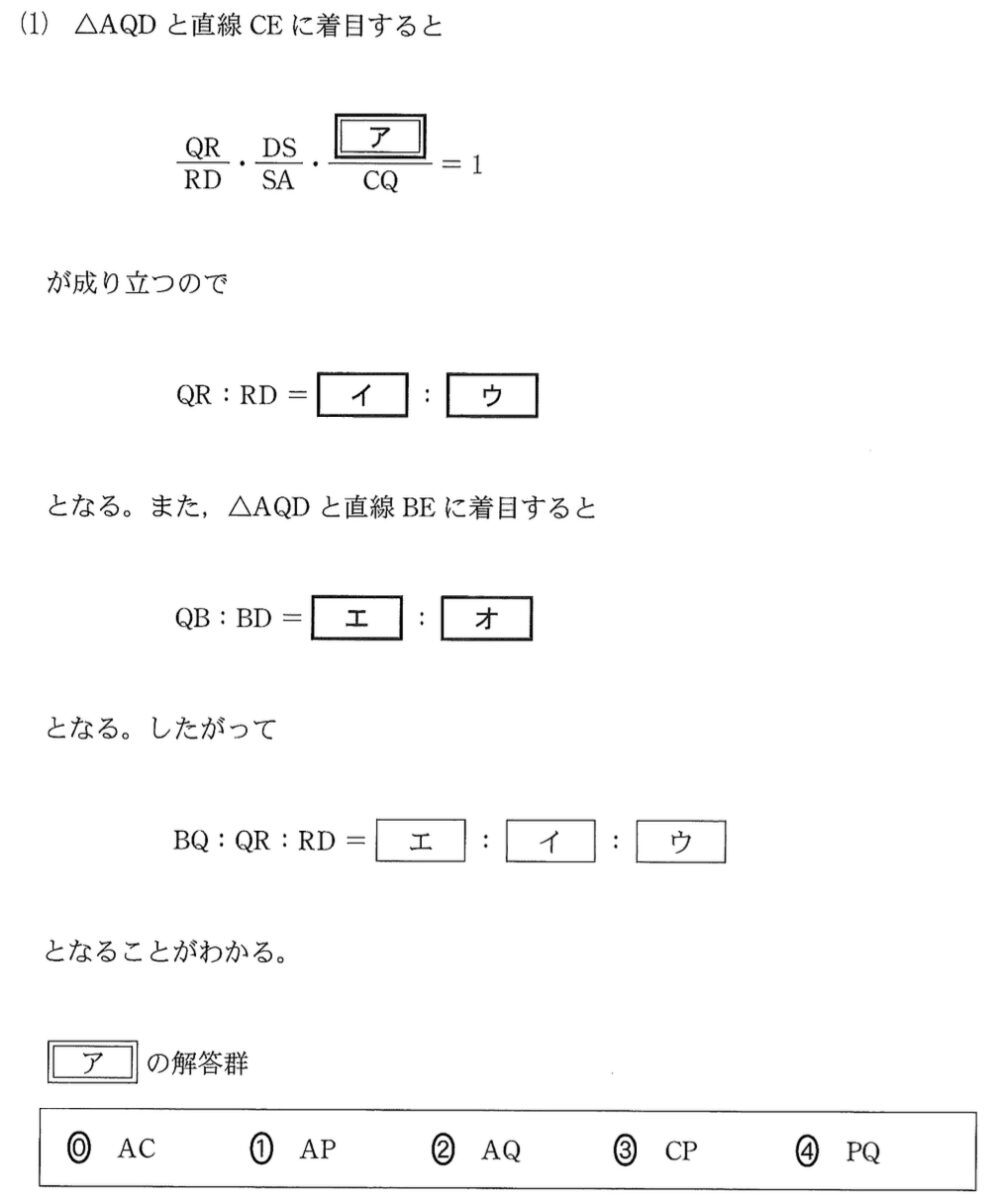
\(\displaystyle\frac{QR}{RD}\times\displaystyle\frac{DS}{SA}\times\displaystyle\frac{AC}{CQ}=1\) ・・・《ア：⓪》
が成り立つので，
\(\displaystyle\frac{QR}{RD}\times\displaystyle\frac{3}{2}\times\displaystyle\frac{8}{3}=1\)
よって \(\displaystyle\frac{QR}{RD}=\displaystyle\frac{1}{4}\) より
\(QR：RD=1：4\) ・・・《イウ》
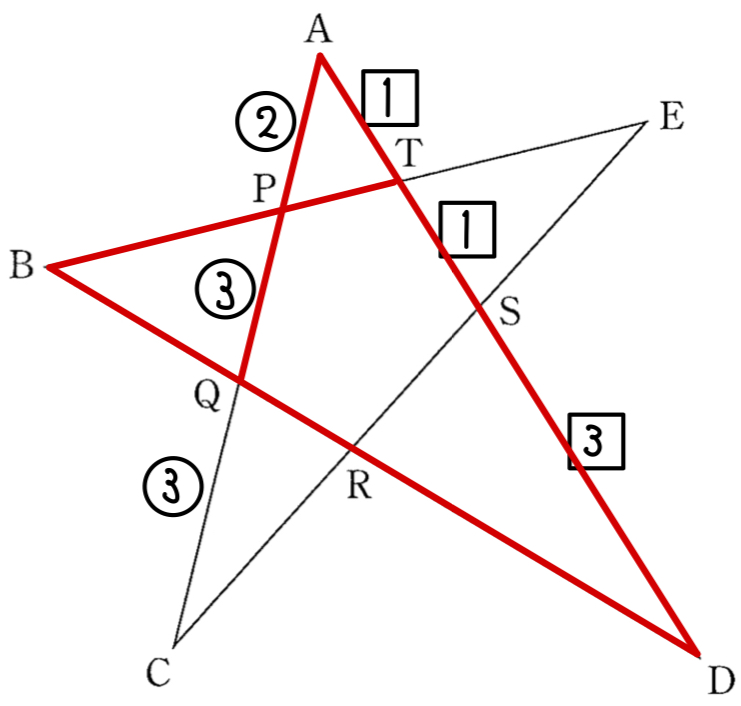メネラウスの定理より
\(\displaystyle\frac{QB}{BD}\times\displaystyle\frac{DT}{TA}\times\displaystyle\frac{AP}{PQ}=1\)
が成り立つので，
\(\displaystyle\frac{QB}{BD}\times\displaystyle\frac{4}{1}\times\displaystyle\frac{2}{3}=1\)
よって \(\displaystyle\frac{QB}{BD}=\displaystyle\frac{3}{8}\) より
\(QB：BD=3：8\) ・・・《エオ》
したがって，\(BQ：QR：RD=3：1：4\) となることがわかる．
(２)の(ⅰ)(ⅱ)問題《カ～シ》
(２)の(ⅰ)(ⅱ)解答・解説《カ～シ》
(ⅰ) \(AT=x\) とすると，\(AS=2x\) なので
方べきの定理から
\(x\times2x=2\times5\) \(\iff\) \(x^2=5\)
よって \(x=AT=\sqrt{5}\) ・・・《カ》
さらに，\(DR=4\sqrt{3}\) となることがわかる．
実際はやらなくてよいけど確認！
\(RQ=y\) とおくと，\(DR=4y\)，\(DQ=5y\) で方べきの定理より
\(4y\times5y=3\sqrt{5}\times4\sqrt{5}\) \(\iff\) \(y=\sqrt{3}\)
ゆえに\(DR=4y=4\sqrt{3}\) となることがわかる．
(ⅱ)まず \(AQ\cdot CQ=5\cdot 3=15\) かつ \(BQ\cdot DQ=3\sqrt{3}\cdot 5\sqrt{3}=\)\(45\) ・・・《キク》
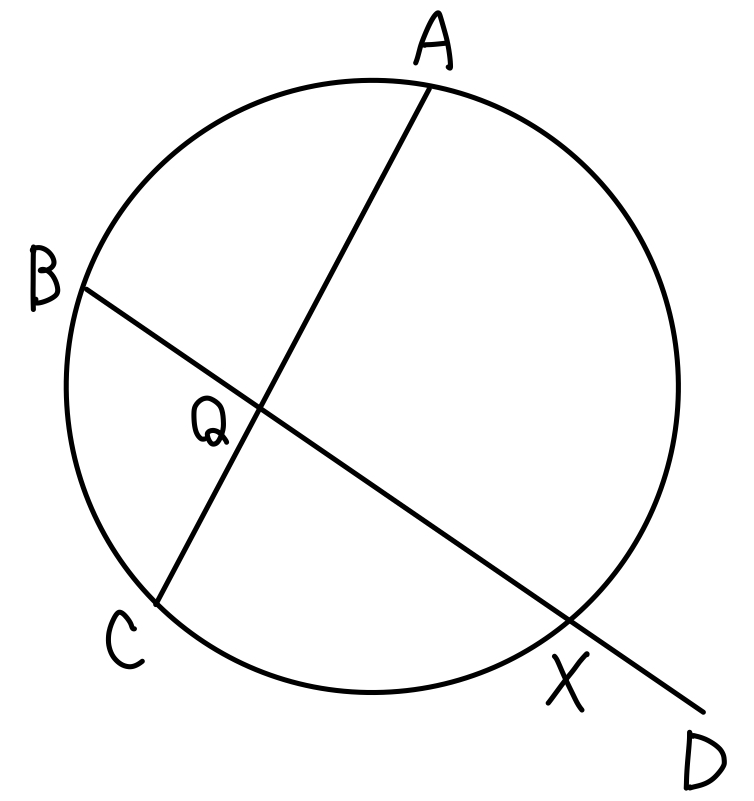\( AQ\cdot CQ< BQ\cdot DQ \) ・・・《ケ：⓪》
方べきの定理より
\( AQ\cdot CQ=BQ\cdot XQ \) ・・・《コ：①》
が成り立つ．上の2式の左辺は同じなので，\(XQ<DQ\) ・・・《サ：⓪》が得られる．
したがって，点 \(D\) は \(3\) 点 \(A\)，\(B\)，\(C\) を通る円の外部・・・《シ：②》にある．
(２)の(ⅲ)問題《スセ》
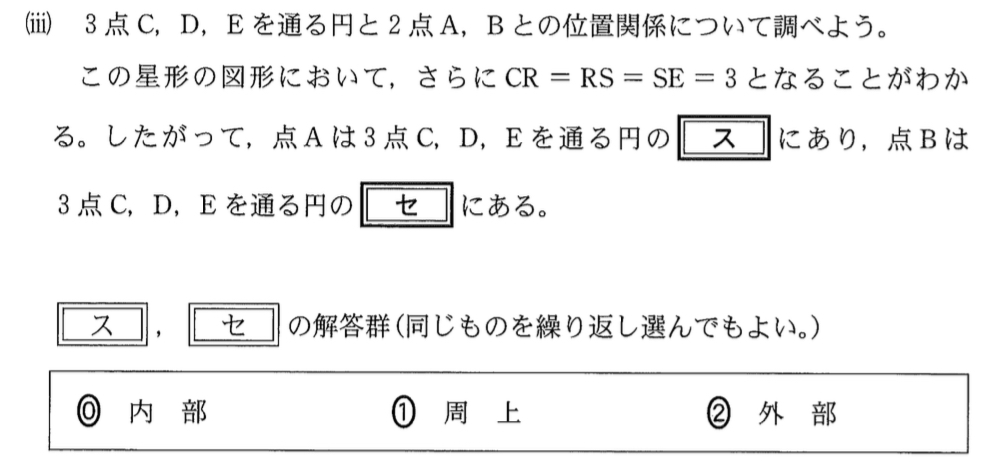
(２)の(ⅲ)解答・解説《スセ》
\(CR=RS=SE=3\) となることがわかる．
(ⅱ)と同様に考えていく
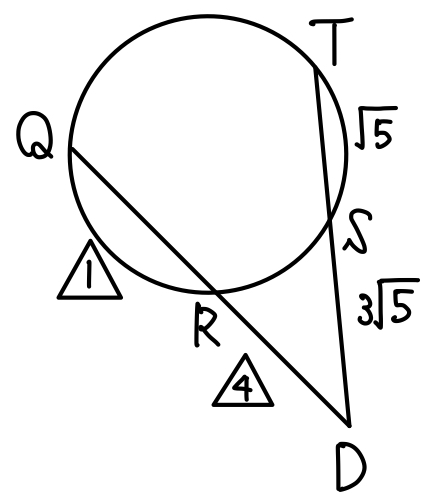
\(DS\times SA=3\sqrt{5}\times2\sqrt{5}=30\)
\(CS\times SE=6\times3=18\)
\( DS\times SA > CS\times SE \) より点 \(A\) は \(3\) 点 \(C\)，\(D\)，\(E\) を通る円の外部・・・《ス：②》
\(DR\times RB=4\sqrt{3}\times4\sqrt{3}=48\)
\(CR\times RE=3\times6=18\)
\( DR\times RB > CR\times RE \) より点 \(B\) は \(3\) 点 \(C\)，\(D\)，\(E\) を通る円の外部・・・《セ：②》
コメント