(1)問題《ア~ス》

(1)解答・解説《ア~ス》
\(m=2\) のとき,すなわち \(f(x)=3(x-1)(x-2)\) のときを考える.
(ⅰ) \(f(x)=3(x-1)(x-2)=3(x^2-3x+2)\) より
\(f^{\prime}(x)=3(2x-3)\)
\(f^{\prime}(x)=0\) となる \(x\) の値は \(x=\displaystyle\frac{3}{2}\) ・・・《アイ》
(ⅱ)\(S(x)=\displaystyle\int^{x}_{0}f(t)dt\)
\(=\displaystyle\int^{x}_{0}(3t^2-9t+6t)dt\) ・・・《ウエ》
\(=\Bigl[t^3-\displaystyle\frac{9}{2}t^2+6t\Bigr]^{x}_{0}\)
\(=x^3-\displaystyle\frac{9}{2}x^2+6x\) ・・・《オ~キ》であるから
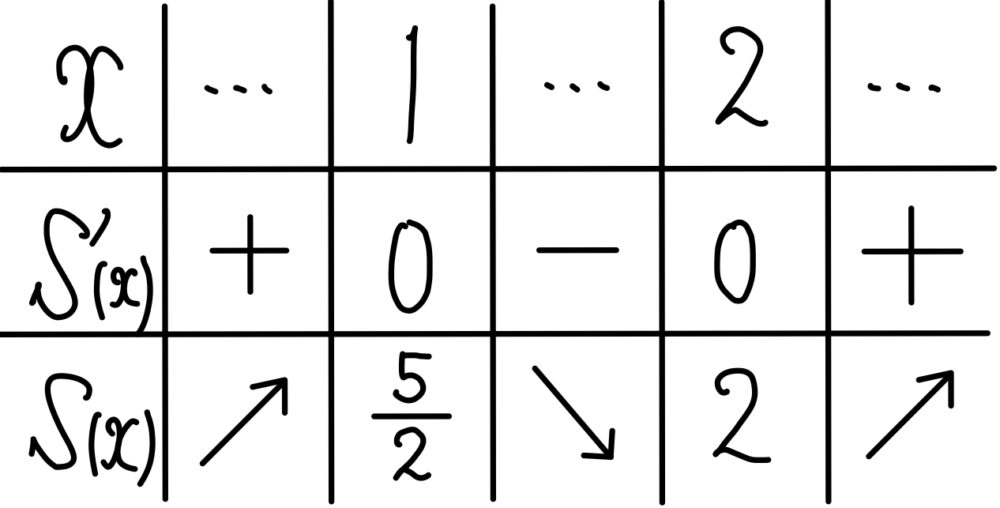 \(S^{\prime}(x)=f(x)=3(x-1)(x-2)\) より
\(S^{\prime}(x)=f(x)=3(x-1)(x-2)\) より
\(x=1\) のとき,\(S(x)\) は極大値 \(\displaystyle\frac{5}{2}\) ・・・《ク~コ》
\(x=2\) のとき,\(S(x)\) は極大値 \(2\) ・・・《サシ》
(ⅲ) \(S^{\prime}(x)=f(x) \) より \(f(3)= S^{\prime}(3)\)
よって,③関数 \(y=S(x)\) のグラフ上の点 \(\left(3,S(3)\right)\) における接線の傾き ・・・《ス》
(2)問題《セ~ツ》
(2)解答・解説《セ~ツ》
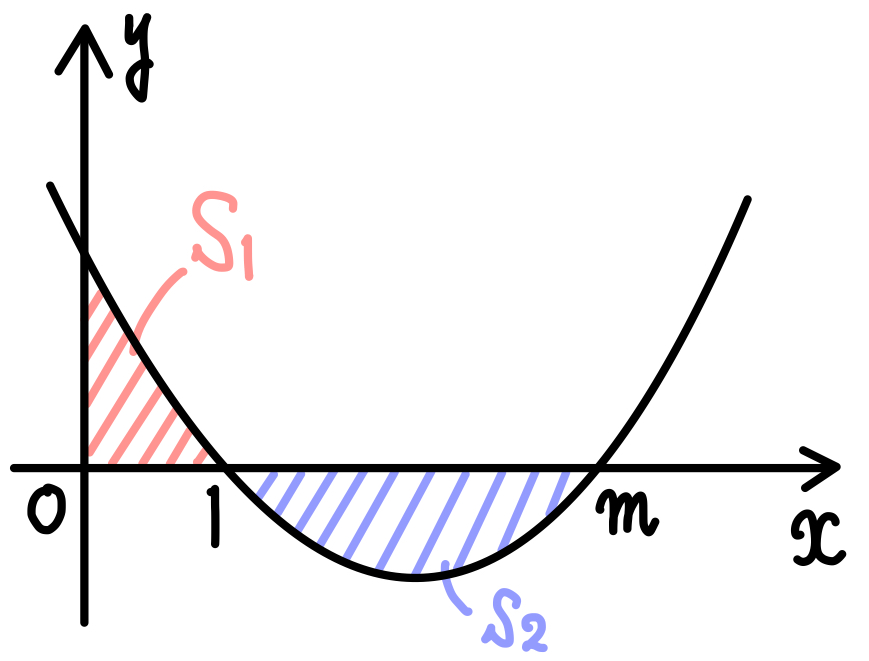 \(f(x)=3(x-1)(x-m)\) ( \(m>1\) ) より
\(f(x)=3(x-1)(x-m)\) ( \(m>1\) ) より
\(S_{1}=\displaystyle\int^{1}_{0}f(x)dx\) ・・・《セ:⓪》
\(S_{2}=\displaystyle\int^{m}_{1}\left\{-f(x)\right\}dx\) ・・・《ソ:⑤》
\(S_{1}=S_{2}\) のとき
\(S_{1}-S_{2}=0\)
\(\displaystyle\int^{1}_{0}f(x)dx -\displaystyle\int^{m}_{1}\left\{-f(x)\right\}dx =0\)
\(\displaystyle\int^{1}_{0}f(x)dx +\displaystyle\int^{m}_{1}f(x) dx =0\)
\(\displaystyle\int^{m}_{0}f(x)dx=0 \) ・・・《タ:①》
このとき
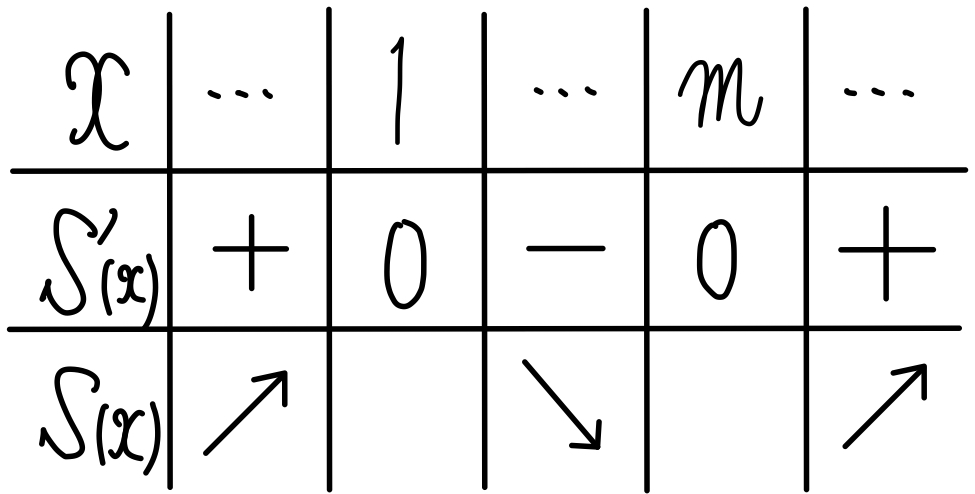 \(S^{\prime}(x)=f(x)=0\) より \(x=1,m\) で
\(S^{\prime}(x)=f(x)=0\) より \(x=1,m\) で
\(S(m)= \displaystyle\int^{m}_{0}f(x)dx=0\) のとき,
\(y=S(x)\) の極小値が \(0\) となることがわかる.
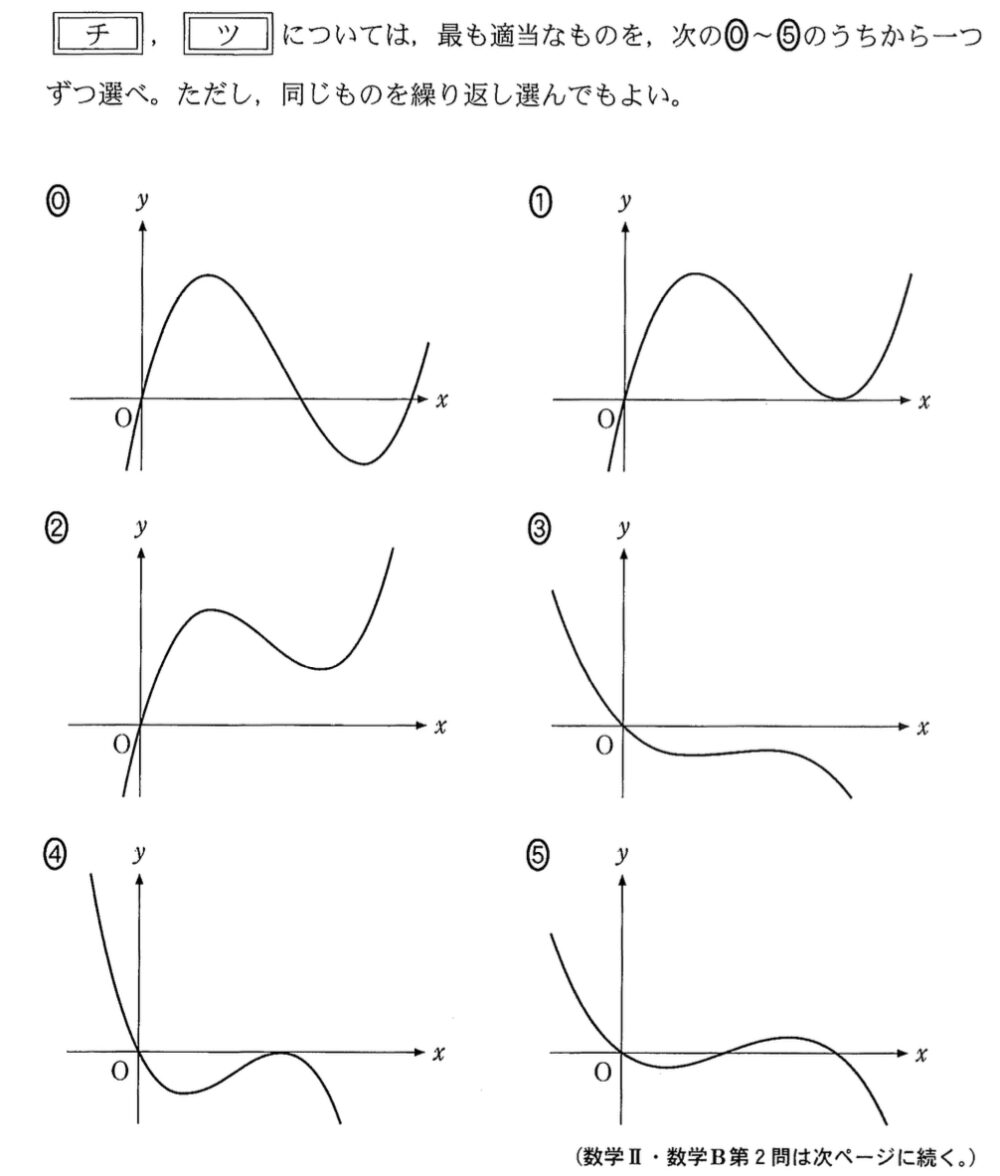
よってそれを満たすグラフは ① ・・・《チ》
\(S_{1}>S_{2}\) のとき
\(S_{1}-S_{2}=S(m)>0\) なので
\(y=S(x)\) の極小値が正の値となることがわかる.
よってそれを満たすグラフは ② ・・・《ツ》
(3)問題《テ~ネ》
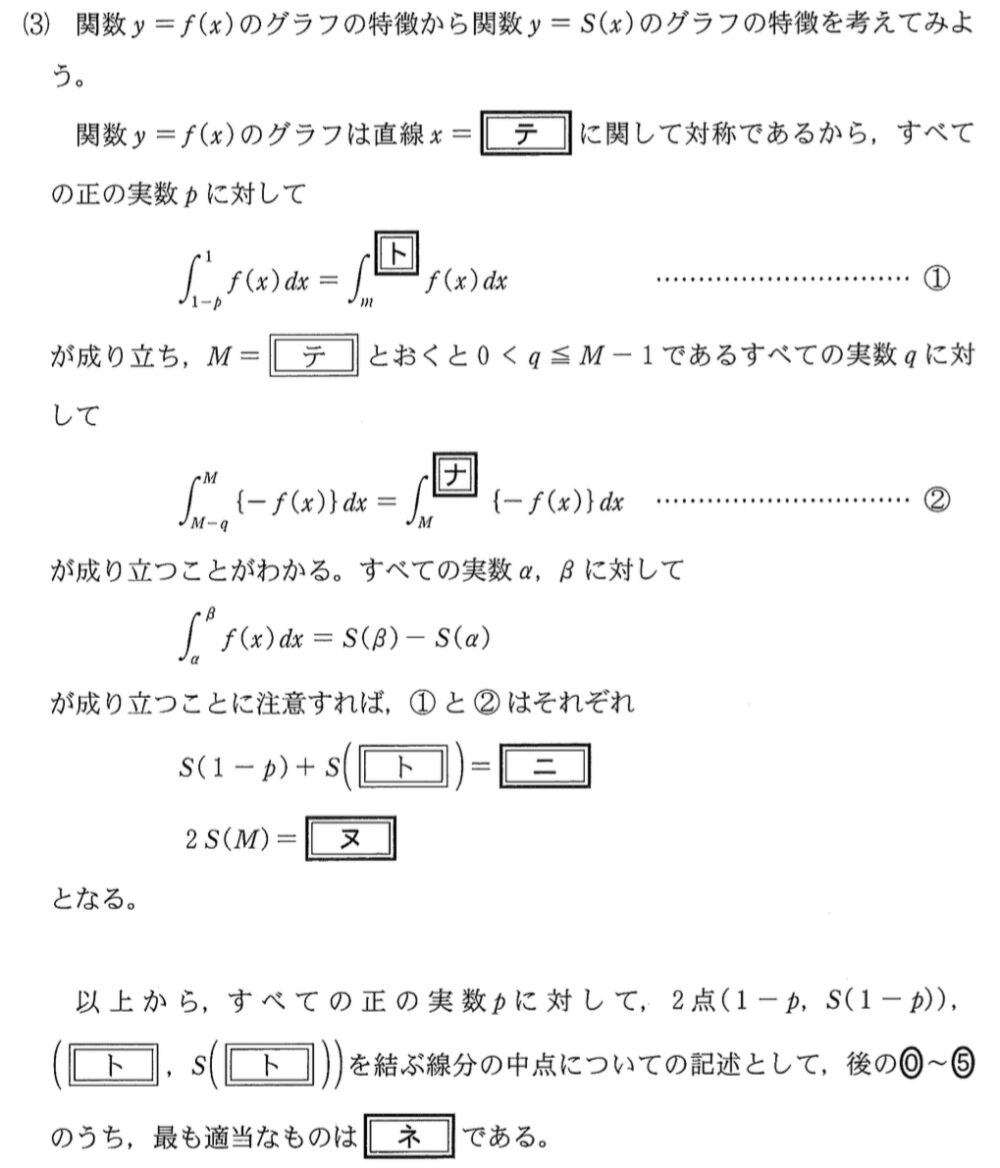
(3)解答・解説《テ~ネ》
\(y=f(x)=3(x-1)(x-m)\) のグラフは
直線(軸) \(x=\displaystyle\frac{m+1}{2}\) ・・・《テ:③》に関して対称であるから、
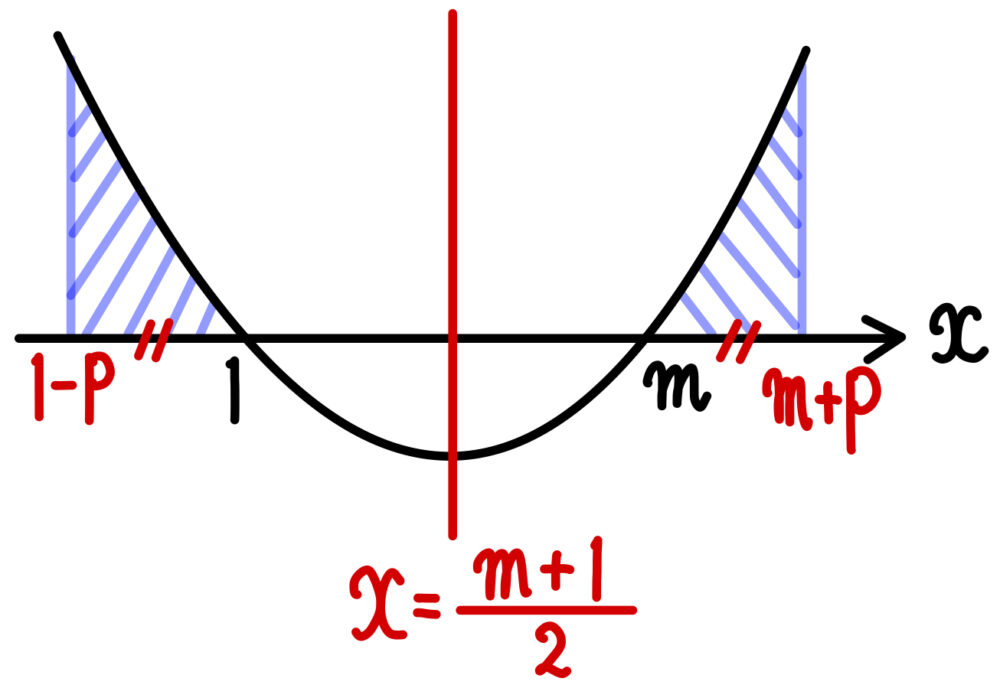 すべての正の実数 \(p\) に対して
すべての正の実数 \(p\) に対して
\(\displaystyle\int^{1}_{1-p}f(x)dx=\displaystyle\int^{m+p}_{m}f(x)dx \) ・・・① 《ト:④》
が成り立ち,\(M=\displaystyle\frac{m+1}{2}\) とおくと
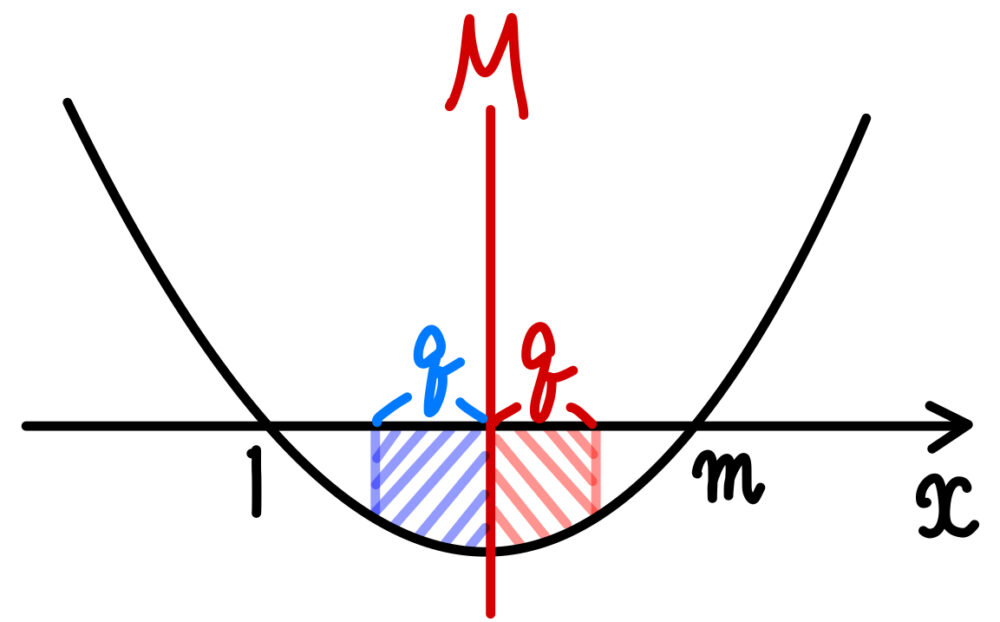 \(0<q≦M-1\) であるすべての実数 \(q\) に対して
\(0<q≦M-1\) であるすべての実数 \(q\) に対して
\(\displaystyle\int^{M}_{M-q}\left\{-f(x)\right\}dx=\displaystyle\int^{M+q}_{M}\left\{-f(x)\right\}dx \) ・・・② 《ナ:②》
が成り立つことがわかる.
\(\displaystyle\int^{\beta}_{\alpha}f(x)dx=S(\beta)-S(\alpha)\) が成り立つことに注意すれば
①より
\(\displaystyle\int^{1}_{1-p}f(x)dx=\displaystyle\int^{m+p}_{m}f(x)dx \)
\(S(1)-S(1-p)=S(m+p)-S(m)\)
\(S(1-p)+S(m+p)=S(1)+S(m)\) ・・・《ニ:⓪》
②より
\(\displaystyle\int^{M}_{M-q}\left\{-f(x)\right\}dx=\displaystyle\int^{M+q}_{M}\left\{-f(x)\right\}dx \)
\(-S(M)+S(M-q)=-S(M+q)+S(M)\)
\(2S(M)= S(M+q)+ S(M-q)\) ・・・《ヌ:④》
以上から
\(2\) 点 \(\left(1-p,S(1-p)\right)\) ,\(\left(m+p,S(m+p)\right)\) を結ぶ線分の中点は
\(\left(\displaystyle\frac{m+1}{2},\displaystyle\frac{S(1-p)+S(m+p)}{2}\right)\)
\(M=\displaystyle\frac{m+1}{2}\),\(S(1-p)+S(m+p)=S(1)+S(m)\) より
\(\left(M,\displaystyle\frac{ S(1)+S(m)}{2}\right)\) なので
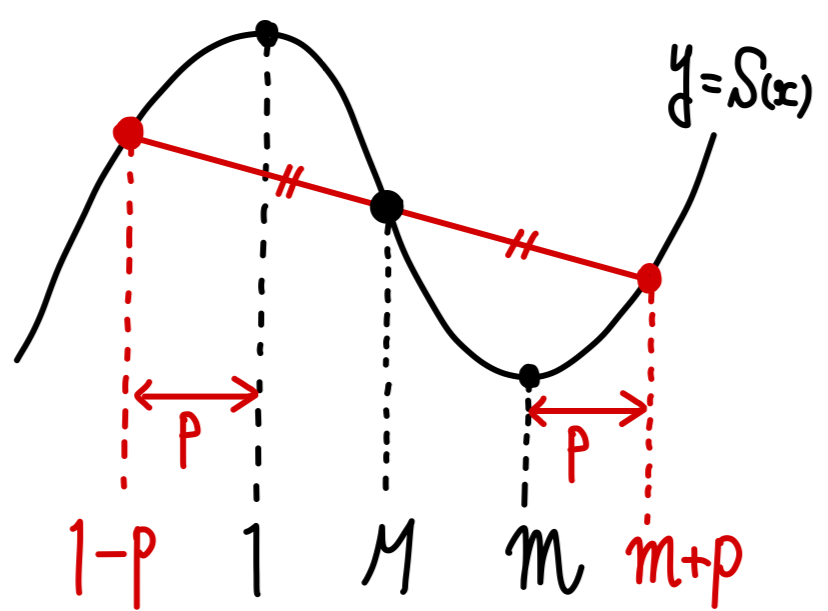 中点は \(p\) の値によらず一つに定まり,関数 \(y=S(x)\) のグラフ上にある・・・《ネ:②》
中点は \(p\) の値によらず一つに定まり,関数 \(y=S(x)\) のグラフ上にある・・・《ネ:②》









コメント