【2024共通テスト(第１日程)】数学ⅡB：第５問　空間ベクトル｜ねじれの位置にある２直線、成分、内積

(１)問題《ア～オ》

\(A(2,7,-1)\) ，\(B(3,6,0)\) ，\(C(-8,10,-3)\) ，\(D(-9,8,-4)\) より

\(\overrightarrow{AB}=(1,-1,1)\) ・・・《ア～エ》

\(\overrightarrow{CD}=(-1,-2,-1)\)

よって \(\overrightarrow{AB}\cdot\overrightarrow{CD}=-1+2-1=\)\(0\) ・・・《オ》

点 \(P\) が \(l_{1}\) 上にあるので，

\(\overrightarrow{AP}=s\overrightarrow{AB}\) を満たす実数 \(s\) があり

\(\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}=\)\(\overrightarrow{OA}+ s\overrightarrow{AB}\) ・・・《カ》なので

\(\overrightarrow{OP}=(2,7,-1)+s(1,-1,1)=(s+2,-s+7,s-1)\)

よって \(\left|\overrightarrow{OP}\right|^2=(s+2)^2+(-s+7)^2+(s-1)^2\)

これを整理すると，

\(\left|\overrightarrow{OP}\right|^2=3s^2-12s+54\) ・・・《キ～サ》

\(\left|\overrightarrow{OP}\right|^2=3(s-2)^2+42\) より

\(s=2\) ・・・《ス》のとき\(\left|\overrightarrow{OP}\right|\) が最小となることがわかる．

また，\(\left|\overrightarrow{OP}\right|\) が最小となるとき，直線 \(OP\) と \(l_{1}\) の関係に着目すると，\(\overrightarrow{OP}\cdot\overrightarrow{AB}=0\) ・・・《シ》

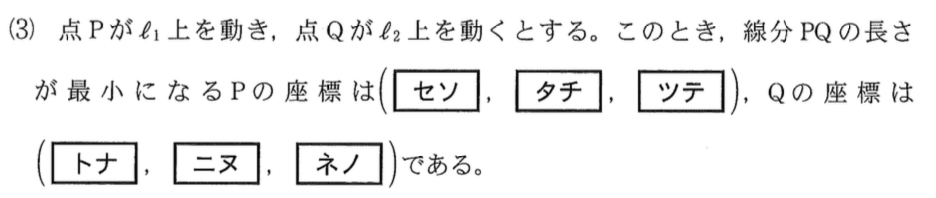
点 \(P\) が \(l_{1}\) 上を動き，点 \(Q\) が \(l_{2}\) 上を動くとする．このとき，線分 \(PQ\) の長さが最小となるのは

\(PQ\) ⊥ \(l_{1}\) かつ \(PQ\) ⊥ \(l_{2}\)

つまり，\(PQ\) ⊥ \(AB\) かつ \(PQ\) ⊥ \(CD\) なので

\(\overrightarrow{PQ}\cdot\overrightarrow{AB}=0\) かつ\(\overrightarrow{PQ}\cdot\overrightarrow{CD}=0\)

ここで点 \(Q\) が \(l_{2}\) 上にあるので，

\(\overrightarrow{AQ}=t\overrightarrow{CD}\) を満たす実数 \(t\) があり

\(\overrightarrow{OQ}=\overrightarrow{OC}+ t\overrightarrow{CD}\) なので

\(\overrightarrow{OQ}=(-8,10,-3)+t(-1,-2,-1)=(-t-8,-2t+10,-t-3)\)

\(\overrightarrow{OP}=(2,7,-1)+s(1,-1,1)=(s+2,-s+7,s-1)\) より

\(\overrightarrow{PQ}=(-s-t-10,s-2t+3,-s-t-2)\)

\(\overrightarrow{PQ}\cdot\overrightarrow{AB}=0\) のとき

\((-s-t-10)-(s-2t+3)+(-s-t-2)=0\) \(\iff\) \(s=-5\)

\(\overrightarrow{PQ}\cdot\overrightarrow{CD}=0\) のとき

\(-(-s-t-10)-2(s-2t+3)-(-s-t-2)=0\) \(\iff\) \(t=-1\)

したがって，\(P(-3,12,-6)\)，\(Q(-7,12,-2)\) ・・・《セ～ノ》