1990京都大学【整数問題・素数】B=60、bは整数、a、cは素数のとき、△ABCは正三角形

整数問題のPoint

整数問題は3つのアプローチで！

まず整数問題すべてに共通して言えるPointは

整数問題の多くが、上の１から３のいずれかで処理できます。

この３つのPointは絶対に頭の中に叩き込んでください！

素数は積の形に弱い！

(素数) ＝ (積の形) に変形できれば、素数の約数は \(1\) か自分自身しかないため、大きく可能性を絞ることができます！

解答

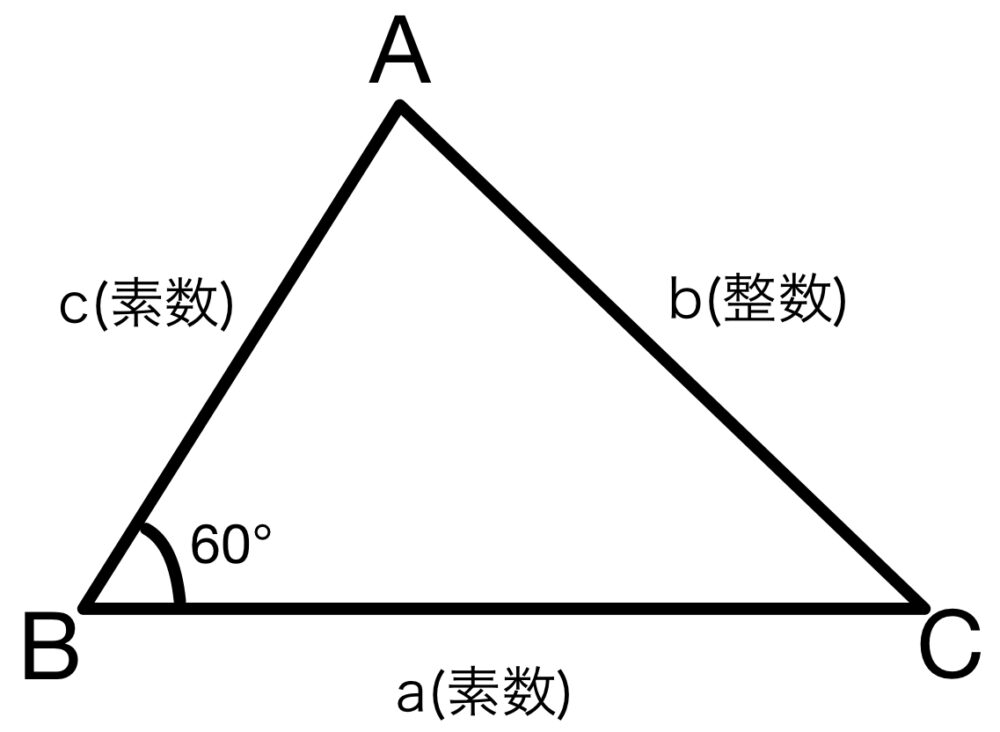
\(a≧c\) として一般性を失わないため、以下では

\(a≧c>0\) ・・・①　とする．

余弦定理より、

\(b^2=a^2+c^2-2ac\cos 60°=a^2+c^2-ac\)

\(b^2=a^2-2ac+c^2+ac=(a-c)^2+ac\) より

\(b^2-(a-c)^2=ac\) \(\iff (b+a-c)(b-a+c)=ac\) ・・・②

\(a\)、\(b\)、\(c\) は三角形の \(3\) 辺であるから、

\(b+a-c>0\)、\(b-a+c>0\) であり、

また①より、\(b+a-c≧b-a+c\) 、さらに \(a\)、\(c\) は素数であるから、②を満たすのは

（ア）\(\begin{cases}b+a-c=ac\\b-a+c=1 \end{cases}\)

（イ）\(\begin{cases}b+a-c=a\\b-a+c=c \end{cases}\)

（ア）のとき、差をとると

\(2a-2c=ac-1\)

\((a+2)(c-2)=-3\)

\(a+2>c-2>-2\) より \(a+2=3\)、\(c-2=-1\)

したがって、\(a=c=1\)

これは素数であることに反する．

（イ）のとき

\(a=b=c\) となり、三角形 \(ABC\) は正三角形となる．

（ア）、（イ）より題意は示された．