【1999京都大学】
放物線 \(y=x^2\) の上を動く \(2\) 点 \(P\) , \(Q\) があって,この放物線と線分 \(PQ\) が囲む部分の面積が常に \(1\) であるとき,\(PQ\) の中点が \(R\) が描く図形の方程式を求めよ.
放物線と直線で囲まれた図形の面積(1/6公式)
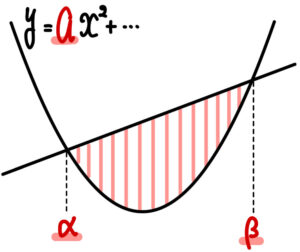 放物線 \(y=ax^2+\cdots\) と放物線上の点で \(x=\alpha\) , \(\beta\) を通る直線によって囲まれた図形の面積は
放物線 \(y=ax^2+\cdots\) と放物線上の点で \(x=\alpha\) , \(\beta\) を通る直線によって囲まれた図形の面積は
\(S=\displaystyle\frac{|a|}{6}(\beta-\alpha)^3\)
※ 頻出・重要公式である
\(\displaystyle\int^{\beta}_{\alpha}(x-\alpha)(x-\beta)dx=\displaystyle\frac{1}{6}(\beta-\alpha)^3\) を利用する.
この公式の証明については様々な大学で出題されています。
しっかりと証明できるようにしておきましょう!
証明については⏬「2022大阪大学・文」を参考にしてください⏬

解答・解説
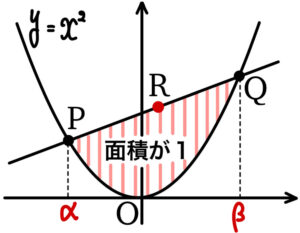
\(P (\alpha,\alpha^2)\) , \(Q (\beta,\beta^2)\) とおく.
( \(\alpha<\beta\) として一般性を失わない )
このとき直線 \(PQ\) の方程式は
\(y-\alpha^2=\displaystyle\frac{\beta^2-\alpha^2}{\beta-\alpha}(x-\alpha)\)
\(y=(\alpha+\beta)x-\alpha\beta\)
よって,放物線と線分 \(PQ\) が囲む部分の面積は
\(\displaystyle\int^{\beta}_{\alpha}\left\{(\alpha+\beta)x-\alpha\beta-x^2\right\} dx\)
\(=\displaystyle\int^{\beta}_{\alpha}-(x-\alpha)(x-\beta) dx\)
\(=\displaystyle\frac{1}{6}(\beta-\alpha)^3\)
これが常に \(1\) となるので,
\(\displaystyle\frac{1}{6}(\beta-\alpha)^3=1\)
\((\beta-\alpha)^3=6\) ・・・①
ここで,\(R (x,y)\) とおくと
\(R\) は線分 \(PQ\) の中点であるから,
\(x=\displaystyle\frac{\alpha+\beta}{2}\) , \(y=\displaystyle\frac{\alpha^2+\beta^2}{2}\)
よって,
\(\alpha+\beta=2x\) ・・・②
\(\alpha^2+\beta^2=2y\) ・・・③
③より
\((\alpha+\beta)^2-2\alpha\beta=2y\)
②を代入すると,\(\alpha\beta=2x^2-y\) ・・・④
①より,\(\left\{(\beta-\alpha)^2\right\}^{\frac{3}{2}}=6\) より
\((\alpha+\beta)^2-4\alpha\beta=6^{\frac{2}{3}}\)
②,④を代入すると
\((2x)^2-4(2x^2-y)=\sqrt[3]{36}\)
したがって,\(y=x^2+\displaystyle\frac{\sqrt[3]{36}}{4}\)







コメント