2000 東京大学-文系 第2問
\(xy\) 平面内の領域 \(-1≦x≦1\)、\(-1≦y≦1\) において
\(1-ax-by-axy\)
の最小値が正となるような定数 \(a\)、\(b\) を座標とする\(( a , b )\) の範囲を図示せよ.
2変数関数の考え方について
2変数関数のMax・min
👉1文字固定(予選決勝法)
2変数関数の最大・最小値に関する基本的な考え方に、予選決勝法と言うものがあります。
これは受験数学では有名解法であり、様々な分野で出題されます。
今まで一度も2変数関数について扱ったことがない人は、
を一度ご覧ください。基本的な考え方を例題を交えて説明しています。
考え方・解答
\(f( x , y )=1-ax-by-axy\) とおく.
\(y\) を固定して考える(\(x\) について降べきの順に並べる)と、
\( f( x , y )=-a(y+1)x-by+1\)
\( f( x , y ) \) は \(x\) の高々 1 次関数
(※高々 1 次関数・・・1次関数or定数関数)
つまり、考えられる図の形は、
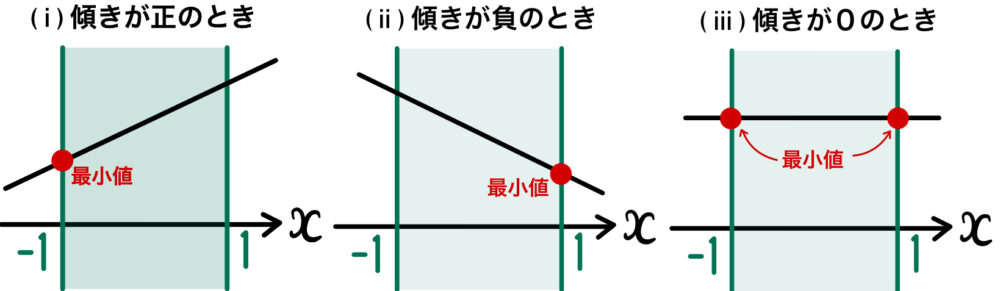
(ⅰ) 傾きが正の直線
(ⅱ) 傾きが負の直線
(ⅲ) 傾きが0の直線 のいずれか
\(-1≦x≦1\) において、(ⅰ)~(ⅲ)を考えると、
最小値は \( f( -1 , y ) \) または \( f( 1 , y )\)
つまり、\( f( -1 , y )>0\) かつ \( f(1 , y )>0\) を満たせばよい
\( f( -1 , y )=a(y+1)-by+1=(a-b)y+a+1>0\)
\( f( 1 , y )=-a(y+1)-by+1=-(a+b)y-a+1>0\)
を満たせばよい

ここまでで、予選が終了。
ここから \(y\) の固定を解除!
つまり決勝戦を行おう!(\(y\) について考える)
\(f( -1 , y )\) や \(f( 1 , y )\) は \(y\) の高々 1 次関数
先ほどと同様に考え、
\(f( -1 , -1 )>0\) かつ \(f( -1 , 1 ) >0\) かつ \(f( 1 , -1 ) >0\) かつ \(f( 1 , 1 ) >0\)
を満たせばよい.
\(\begin{cases}f( -1 , -1 )=b+1>0\\f( -1 , 1 )=2a-b+1>0\\f( 1 , -1 )=b+1>0\\(f( 1 , 1 )=-2a-b+1>0 \end{cases}\)
\(\begin{cases} b>-1\\ b<2a+1\\ b<-2a+1 \end{cases}\)
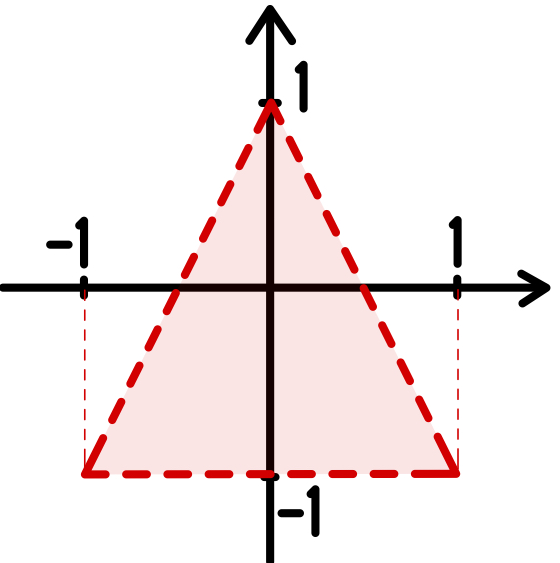
求める領域は図の赤の領域で、境界線は含まない.
最後に
2変数関数など、大学受験では頻出テーマであっても、学校の授業ではあまり扱われないテーマは多数あります。
そのような頻出テーマをメインに、他の記事で扱っています。よかったら受験勉強の参考にしてください。
また、〇〇について扱って欲しいなど、ご要望がありましたら、遠慮なくコメント・問い合わせ・Twitterなどからご連絡ください。










コメント