【2009東京大学・理系・第5問】
(1) 実数 \(x\) が \(-1<x<1\) ,\(x\not=0\) をみたすとき,次の不等式を示せ.
\((1-x)^{1-\frac{1}{x}}<(1+x)^{\frac{1}{x}}\)
(2) 次の不等式を示せ.
\(0.9999^{101}<0.99<0.9999^{100}\)
解答・解説
(1) \((1-x)^{1-\frac{1}{x}}<(1+x)^{\frac{1}{x}}\)
\(-1<x<1\) より,\(1-x>0\),\(1+x>0\) なので
与式の両辺に自然対数をとると
\((1-x)^{1-\frac{1}{x}}<(1+x)^{\frac{1}{x}}\)
\(\iff\) \(\log{(1-x)^{1-\frac{1}{x}}}<\log{(1+x)^{\frac{1}{x}}}\)
\(\iff\) \(\left(1-\displaystyle\frac{1}{x}\right)\log{(1-x)}<\displaystyle\frac{1}{x}\log{(1+x)}\)
\(\iff\) \(\log(1-x)<\displaystyle\frac{1}{x}\left\{\log(1+x)+\log(1-x)\right\}\)
\(\iff\) \(\log(1-x)<\displaystyle\frac{1}{x}\log(1-x^2)\)
\(\iff\) \(\begin{cases}x\log(1-x)<\log(1-x^2) (0<x<1\text{のとき})\\x\log(1-x)>\log(1-x^2) (-1<x<0のとき)\end{cases}\)
を示せばよい.
ここで \(f(x)=\log(1-x^2)-x\log(1-x)\) とおく.
\(f^{\prime}(x)=\displaystyle\frac{-2x}{1-x^2}-\log(1-x)+\displaystyle\frac{x}{1-x}\)
=\(-1+\displaystyle\frac{1}{1+x}-\log(1-x)\)

\(f^{\prime}(x)=0\) を満たす \(x\) の値を考えて増減表を考えたいけど・・・

\(f^{\prime}(x)\) で解決しない場合は,さらに微分(\(f^{\prime\prime}(x)\)) を考えましょう!
\(f^{\prime\prime}(x)=\displaystyle\frac{-1}{(1+x)^2}+\displaystyle\frac{1}{1-x}=\displaystyle\frac{x(x+3)}{(1+x)^2(1-x)}\) より
| \(x\) | \(-1\) | ・・・ | \(0\) | ・・・ | \(1\) |
| \(f^{\prime\prime}(x)\) | ー | \(0\) | + | ||
| \(f^{\prime}(x)\) | ↘️ | \(0\) | ↗️ |
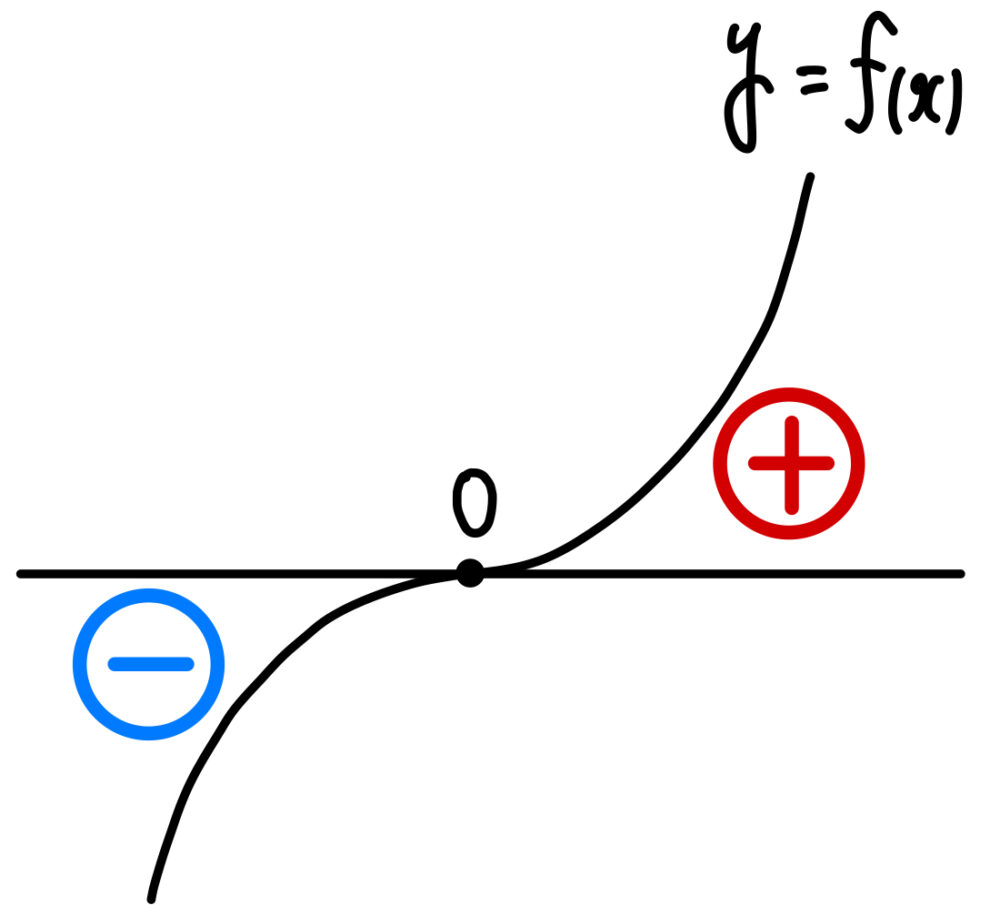 よって増減表より,\(-1<x<1\),\(x\not=0\) において
よって増減表より,\(-1<x<1\),\(x\not=0\) において
\(f^{\prime}(x)>0\) であるから,\(f(x)\) は単調に増加する.
また,\(f(0)=0\) であるから,
\(-1<x<0\) のとき \(f(x)<0\)
\(0<x<1\) のとき \(f(x)>0\)
となり,題意は示された.
(2) \(0.9999^{101}<0.99<0.9999^{100}\)
(1)の結果において,両辺に \((1-x)^{\frac{1}{x}}\) (>0) をかけると
\(1-x<\left\{(1+x)(1-x)\right\}^{\frac{1}{x}}=(1-x^2)^{\frac{1}{x}}\)
この式に \(x=0.01\) を代入すると
\(0.99<0.9999^{100}\) ・・・①
また同様に (1)の結果において両辺に \((1+x)^{1-\frac{1}{x}}\) (>0) をかけると
\((1-x^2)^{1-\frac{1}{x}}<1+x\)
この式に \(x=-0.01\) を代入すると
\(0.9999^{101}<0.99\) ・・・②
①,②より,\(0.9999^{101}<0.99<0.9999^{100}\)








コメント