【2021上智大学・理工】7の35乗は何桁？｜常用対数(桁数)・近似値

【2021上智大学・理工】

(１)　不等式 \(\displaystyle\frac{k-1}{k}<\log_{10}{7}<\displaystyle\frac{k}{k+1}\) を満たす自然数 \(k\) を求めよ．

(２)　\(7^{35}\) は何桁の整数か．

《参考》常用対数の近似値

(１)では、常用対数の近似値を求める問題ですが、おおよその値を覚えておくと答えの検討をつけることができるため、便利です！

《参考》常用対数の近似値

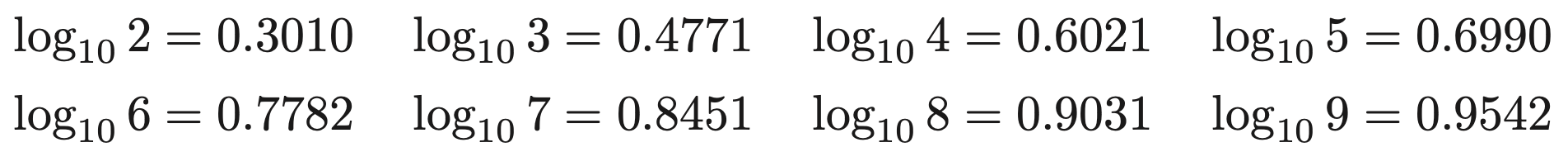
\(\log_{10}{7}=0.8451\) であり、

\(\displaystyle\frac{5}{6}=0.833\cdots\)、\(\displaystyle\frac{6}{7}=0.857\cdots\) であるから、

\(\displaystyle\frac{5}{6}<\log_{10}{7}<\displaystyle\frac{6}{7}\)

したがって、 \(k=6\) であると答えがわかる．

記述の問題であればもちろんこの解答はダメであるが、私立など答えのみでよければ近似値を覚えておくと便利である。

(１)　\(\displaystyle\frac{k-1}{k}<\log_{10}{7}<\displaystyle\frac{k}{k+1}\) より、

\(10^{\frac{k-1}{k}}<7<10^{\frac{k}{k+1}}\)

よって、\(10^{k-1}<7^k\) かつ \(7^{k+1}<10^k\)

\(10^k\) で割ると

\(\displaystyle\frac{1}{10}<\left(\displaystyle\frac{7}{10}\right)^k\) かつ \(7\cdot \left(\displaystyle\frac{7}{10}\right)^k<1\)

よって、\(\displaystyle\frac{1}{10}<\left(\displaystyle\frac{7}{10}\right)^k<\displaystyle\frac{1}{7}=0.14\cdots\) ・・・①

ここで、\(0.7^2=0.49\)、\(0.7^3=0.343\)、\(0.7^4=0.2401\)、\(0.7^5=0.16807\)、

\(0.7^6=0.16807\times 0.7=0.11\cdots\)、\(0.7^7=0.11\cdots \times 0.7<0.1\) より

①を満たす自然数は \(k=6\)

(２)　(１)より、\(\displaystyle\frac{5}{6}<\log_{10}{7}<\displaystyle\frac{6}{7}\)、

また \(\log_{10}{7^{35}=35\log_{10}{7}}\) より

\(35\times\displaystyle\frac{5}{6}<\log_{10}{7^{35}}<35\times\displaystyle\frac{6}{7}\)、

\(\displaystyle\frac{175}{6}<\log_{10}{7^35}<30\)

よって、\(29<\log_{10}{7^35}<30\) であるから、\(7^{35}\) は \(30\) 桁