【2016京都大学(理)】
四面体 \(OABC\) が次の条件を満たすならば，それは正四面体であることを示せ．
条件：頂点 \(A\) , \(B\) , \(C\) からそれぞれの対面を含む平面へ下ろした垂線は対面の外心を通る．
ただし，四面体のある頂点の対面とは，その頂点を除く他の \(3\) つの頂点がなす三角形のことをいう．
外心とは？
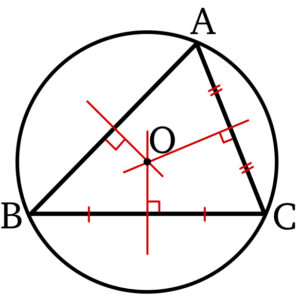三角形の \(3\) 辺の垂直二等分線は \(1\) 点で交わり，その点から各頂点までの距離は等しい．
この \(1\) 点で交わった点 \(O\) を三角形の外心という．
解答
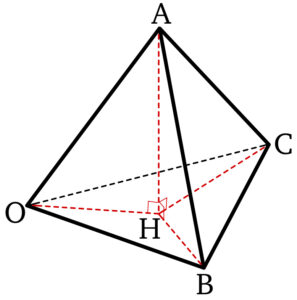頂点 \(A\) から平面 \(OBC\) に下ろした垂線の足を \(H\) とする．
\(AH \perp\) 平面 \(OBC\) より
\(\angle AHO=\angle AHB=\angle AHC=90°\) ・・・①
条件から，点 \(H\) は \(\triangle OBC\) の外心であるから，
\(HO=HB=HC\) ・・・②
①，②と \(AH\) が共通であることから，
\(\triangle AHO≡\triangle AHB≡\triangle AHC\) となり，
\(AO=AB=AC\) ・・・③
同様に，\(B\) , \(C\) を頂点としてそれぞれ考えると
\(BA=BO=BC\) ，\(CA=CO=CB\) ・・・④
③，④より
\(OA=OB=OC=AB=BC=CA\) となりすべての面が正三角形となるから，四面体 \(OABC\) は正四面体となる．
コメント