【2022数学ⅡB】第1問[1](図形と方程式)
(1)問題と解答・解説《ア〜イ》
解答・解説《ア〜イ》
\(x^2+y^2-4x-10y+4≦0\) より
\((x-2)^2+(y-5)^2≦25\)
よって,領域 \(D\) は
中心が点 \((2,5)\) , 半径 \(5\) の円の周および内部 ・・・《ア〜エ》
(2)ー( ⅰ )問題と解答・解説《オ》

解答・解説《オ》
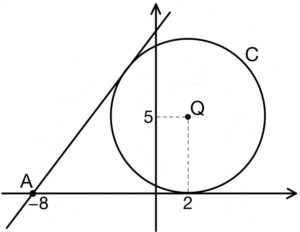
円 \(C\) は,中心 \((2,5)\) , 半径 \(5\) の円であり,
それを図示すると右図のようになる.
よって, \(A (-8 , 0)\) を通る円 \(C\) の接線の \(1\) つは
\(x\) 軸つまり,\(y=0\) ・・・《オ》
(2)ー( ⅱ )問題と解答・解説《カ》

解答・解説《カ》
\(y=k(x+8)\) を \(x^2+y^2-4x-10y+4=0\) に代入しまとめると
\((k^2+1)x^2+(16k^2-10k-4)x+64k^2-80k+4=0\)
を得るので,これが重解をもつ(⓪)とき \(k\) の値が接線の傾きとなる.・・・《オ》
(2)ー( ⅲ )問題と解答・解説《キ〜ケ》
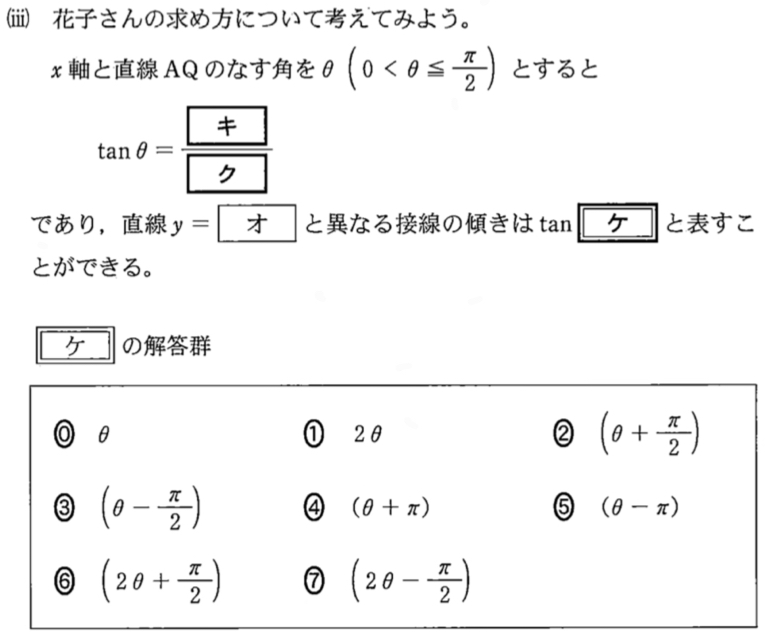
解答・解説《キ〜ケ》
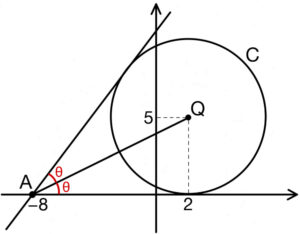
右図より,\(\tan θ=\displaystyle\frac{5}{10}=\)\(\displaystyle\frac{1}{2}\) ・・・《キク》
であり,直線 \(y=0\) と異なる接線の傾きは
\(\tan 2\theta\) (①) ・・・《ケ》
と表すことができる.
(2)ー( ⅲ )問題と解答・解説《コ〜シ》
解答・解説《コ〜シ》
( ⅱ ) の考えについての解答
\((k^2+1)x^2+(16k^2-10k-4)x+64k^2-80k+4=0\) が重解をもつとき
判別式を \(D\) とすると,
\(\displaystyle\frac{D}{4}=(8k^25k-2)^2-(k^2+1)(64k^2-80k+4)=0\)
\(75k^2-100k=0\)
よって,\(k=0,\displaystyle\frac{4}{3}\)
したがって,\(k_{0}=\displaystyle\frac{4}{3}\) ・・・《コサ》
( ⅲ ) の考えについての解答
\(2\) 倍角の公式から
\(\tan 2\theta=\displaystyle\frac{2\tan \theta}{1-\tan^2\theta}\)
\(\tan \theta=\displaystyle\frac{1}{2}\) より
\(k_{0}=\displaystyle\frac{2\times \frac{1}{2}}{1-\left(\frac{1}{2}\right)^2}=\displaystyle\frac{4}{3}\) ・・・《コサ》
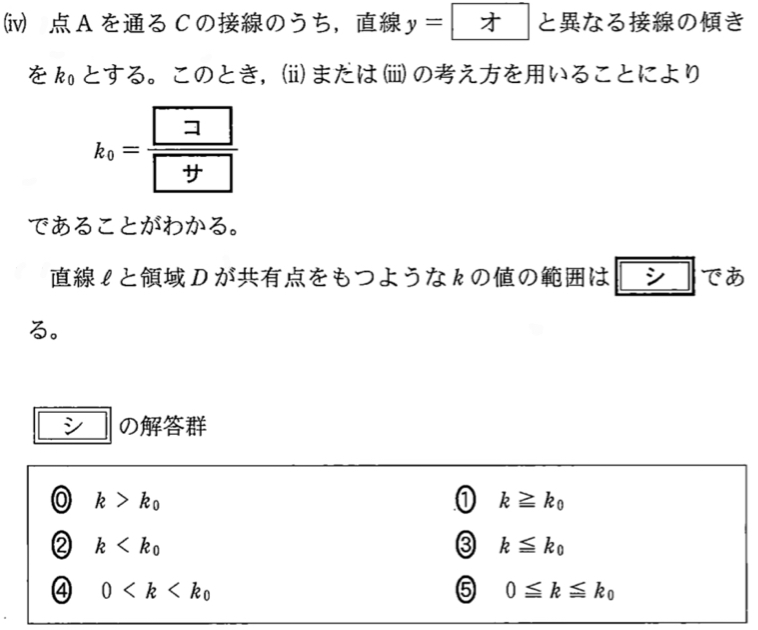
最後に,直線 \(y=k(x+8)\) と領域 \(D\) が共有点をもつような \(k\) の値の範囲は,
\(0≦k≦k_{0}\) ・・・《シ》








コメント