【2022昭和大学・医学部】Ⅱ期・第2問(3)14^100 最高位、桁数、15で割った余り

【2022昭和大学・医学部】Ⅱ期・第２問（３）

\(n=14^{100}\) とし、\(n\) の最高位の数字を \(a\) とする．

次の各問いに答えよ．なお、必要に応じて下記対数表を用いること．

(\(a\))　\(n\) の桁数を求めよ．

(\(b\))　\(a\) の値を求めよ．

(\(c\))　\(a\times n\) を \(15\) で割った余りを求めよ．

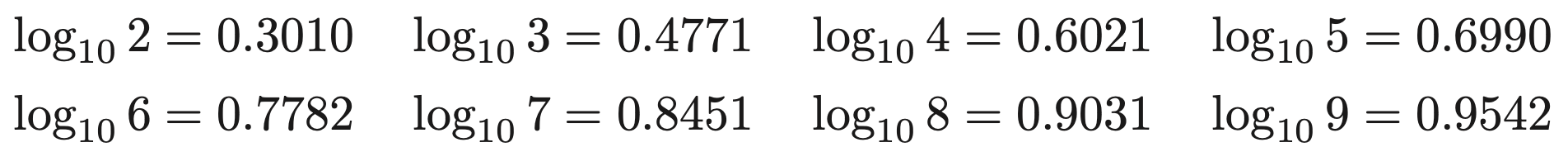
【常用対数】桁数・最高位・一の位の求め方

常用対数を用いた、桁数・最高位・一の位の求め方をこちらの記事にまとめています。参考にしてください！

\(n=14^{100}\) に常用対数をとると、

\(\log_{10}{n}=\log_{10}{14^{100}}=100\log_{10}{14}\)

\(=100\times(\log_{10}{2}+\log_{10}{7})=100\times(0.3010+0.8451)=114.61\)

であるから、

\(114<\log_{10}{n}<115\) \(\iff\) \(10^{114}<n<10^{115}\)

よって、\(n\) は \(115\) 桁の数である．

\(\log_{10}{n}=114.61\) より、

\(n=10^{114.61}=10^{0.61}\times 10^{114}\) ・・・①

ここで、\(0.6021<0.61<0.6990\) より

\(\log_{10}{4}<0.61<\log_{10}{5}\) \(\iff\) \(4<10^{0.61}<5\) ・・・②

①、②より \(n\) の最高位の数字は \(a=4\)

\(a\times n=4\times 14^{100}\) ・・・③

以下では、mod 15 として考えると、\(14≡-1\) であるから、③より

\(a\times n≡4\times(-1)^{100}=4\)

であるから、\(a\times n\) を \(15\) で割った余りは \(4\)

※合同式は整数問題を扱う上で必須アイテムです。

学校で学習していない、使い方に不安がある方は下記の記事を参考に合同式が使えるようにしておきましょう！