【2021京都大学・文】
\(\triangle 0AB\) において，\(OA=3\) , \(OB=2\) , \(\angle AOB=60°\) とする．\(\triangle OAB\) の垂心 \(H\) とするとき，\(\overrightarrow{OH}\) を \(\overrightarrow{OA}\) と \(\overrightarrow{OB}\) を用いて表せ．
垂心とは
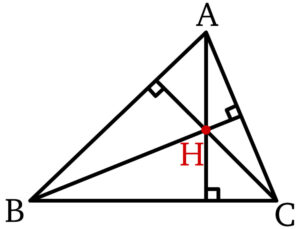垂心とは，三角形の各頂点から対辺におろした垂線の交点
考え方
① 点 \(H\) は \(\triangle OAB\) 上より共面条件
👉 実数 \(s\) , \(t\) を用いて
\(\overrightarrow{OH}=s\overrightarrow{OA}+t\overrightarrow{OB}\) とおける
※ 共面条件についての詳細・例題は「
② 点 \(H\) は垂心
👉 \(OH \perp AB\) かつ \(AH \perp OB\)
⇒ \(\overrightarrow{OH}\cdot\overrightarrow{AB}=0\) かつ \(\overrightarrow{AH}\cdot\overrightarrow{OB}=0\)
解答
\(\triangle 0AB\) において，\(OA=3\) , \(OB=2\) , \(\angle AOB=60°\) とする．\(\triangle OAB\) の垂心 \(H\) とするとき，\(\overrightarrow{OH}\) を \(\overrightarrow{OA}\) と \(\overrightarrow{OB}\) を用いて表せ．
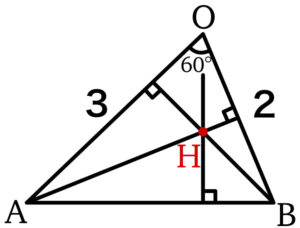
実数 \(s\) , \(t\) を用いて
\(\overrightarrow{OH}=s\overrightarrow{OA}+t\overrightarrow{OB}\) とおける
点 \(H\) は垂心より，\(OH \perp AB\) かつ \(AH \perp OB\)
・\(OH \perp AB\) のとき
\(\overrightarrow{OH}\cdot\overrightarrow{AB}=0\) より
\(\overrightarrow{OH}\cdot(\overrightarrow{OB}-\overrightarrow{OA})=0\)
\((s\overrightarrow{OA}+t\overrightarrow{OB})\cdot(\overrightarrow{OB}-\overrightarrow{OA})\)
\((s-t)\overrightarrow{OA}\cdot\overrightarrow{OB}-s\left| \overrightarrow{OA} \right|^2+t\left| \overrightarrow{OB} \right|^2=0\)
ここで，\(\left|\overrightarrow{OA}\right|=3\) , \(\left|\overrightarrow{OB}\right|=2\) , \(\angle AOB=60°\) より，
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=3\times 2\times \cos 60°=3\) であるから，
\(3(s-t)-9s+4t=0\) \(\iff\) \(t=6s\) ・・・①
・\(AH \perp OB\) のとき
\(\overrightarrow{AH}\cdot\overrightarrow{OB}=0\)
\((\overrightarrow{OH}-\overrightarrow{OA})\cdot\overrightarrow{OB}=0\)
\((s\overrightarrow{OA}+t\overrightarrow{OB}-\overrightarrow{OA})\cdot\overrightarrow{OB}=0\)
\((s-1)\overrightarrow{OA}\cdot\overrightarrow{OB}+t\left|\overrightarrow{OB}\right|^2=0\)
\(3s+4t-3=0\) ・・・②
①，②より，\(s=\displaystyle\frac{1}{9}\) , \(t=\displaystyle\frac{2}{3}\)
したがって，\(\overrightarrow{OH}=\displaystyle\frac{1}{9}\overrightarrow{OA}+\displaystyle\frac{2}{3}\overrightarrow{OB}\)
コメント