【2021お茶の水女子大学・理・第１問】
\(a>b>0\) として，座標平面上の楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) を \(C\) とおく．
\(C\) 上の点 \(P(p_{1},p_{2})\) ( \(p_{2}\not=0\) ) における \(C\) の接線を \(l\)，法線を \(n\) とする．
(１) 接線 \(l\) および法線 \(n\) の方程式を求めよ．
(２) \(2\) 点 \(A(\sqrt{a^2-b^2},0)\) ，\(B(-\sqrt{a^2-b^2},0)\) に対して，法線 \(n\) は \(\angle APB\) の二等分線であることを示せ．
楕円について
楕円の定義
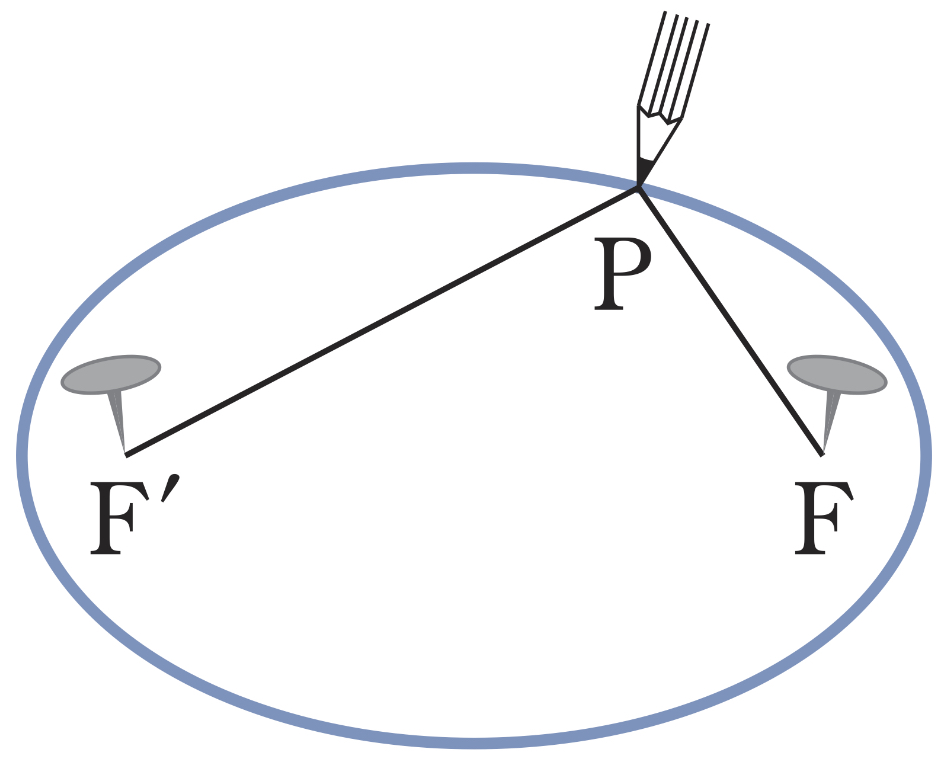
楕円の性質
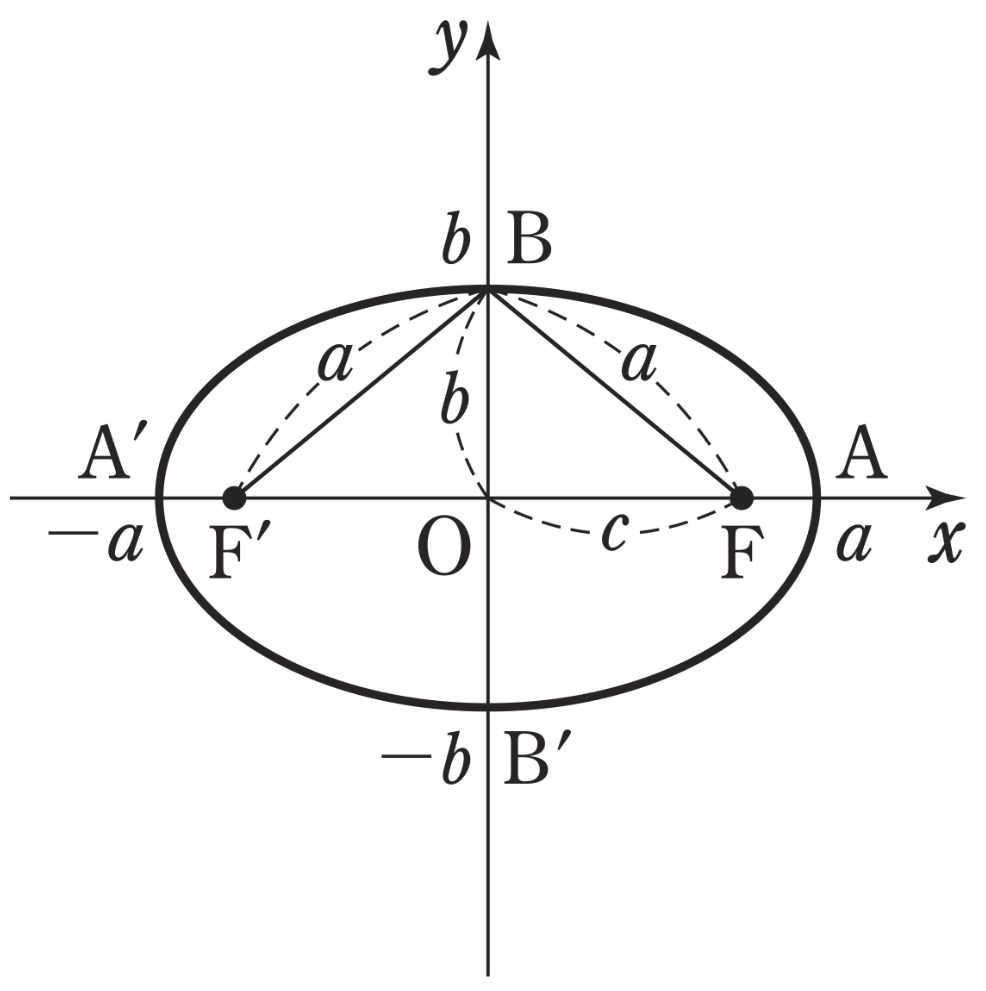楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) (\(a>0\) ，\(b>0\) )
- 中心は原点，長軸の長さは \(2a\)，短軸の長さは \(2b\)
- 焦点は \(2\) 点 \((\sqrt{a^2-b^2},0)\) ，\((-\sqrt{a^2-b^2},0)\)
- 楕円は \(x\) 軸，\(y\) 軸，原点に関して対称である．
- 楕円上の点から \(2\) つの焦点までの距離の和は \(2a\)
楕円の接線の方程式
楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) 上の点 \(P(p_{1},p_{2})\) における楕円の接線の方程式は
\(\displaystyle\frac{p_{1}x}{a^2}+\displaystyle\frac{p_{2}y}{b^2}=1\)
頻出ですから結果は覚えておきましょう！
証明については，下記の(1)の解答を参考に。
解答・解説
(１)
楕円の接線の方程式について
\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) の両辺を \(x\) で微分すると
\(\displaystyle\frac{2x}{a^2}+\displaystyle\frac{2y}{b^2}\displaystyle\frac{dy}{dx}=0\)
\(y\not=0\) のとき \(\displaystyle\frac{dy}{dx}=-\displaystyle\frac{b^2x}{a^2y}\) より
求める接線の傾きは，\(\displaystyle\frac{dy}{dx}=-\displaystyle\frac{b^2p_{1}}{a^2p_{2}}\)
よって，接線の方程式は
\(y-p_{2}=-\displaystyle\frac{b^2p_{1}}{a^2p_{2}}\left(x-p_{1}\right)\)
\(\displaystyle\frac{p_{1}x}{a^2}+\displaystyle\frac{p_{2}y}{b^2}=\displaystyle\frac{p_{1}^2}{a^2}+\displaystyle\frac{p_{2}^2}{b^2}\)
点 \(P(p_{1},p_{2})\) は楕円 \(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) 上の点より，\(\displaystyle\frac{p_{1}^2}{a^2}+\displaystyle\frac{p_{2}^2}{b^2}=1\) より
求める接線の方程式は，\(\displaystyle\frac{p_{1}x}{a^2}+\displaystyle\frac{p_{2}y}{b^2}=1\)
(また，\(y=p_{2}=0\) のとき \(p_{1}=\pm a\) より，接線の方程式は \(x=\pm a\) となり成立．)
楕円の法線の方程式について
・\(p_{1}\not=0\) のとき
\(p_{2}\not=0\) のとき接線の傾きは \(\displaystyle\frac{dy}{dx}=-\displaystyle\frac{b^2p_{1}}{a^2p_{2}}\) より，
法線の傾きは \(\displaystyle\frac{dy}{dx}=\displaystyle\frac{a^2p_{2}}{b^2p_{1}}\)
よって法線の方程式は
\(y-p_{2}=\displaystyle\frac{a^2p_{2}}{b^2p_{1}}\left(x-p_{1}\right)\)
\(a^2p_{2}x-b^2p_{1}y=(a^2-b^2)p_{1}p_{2}\)
・\(p_{1}=0\) のとき
\(p_{2}=\pm b\) で，法線の方程式は \(x=0\) となり成立．
したがって法線の方程式は，\(a^2p_{2}x-b^2p_{1}y=(a^2-b^2)p_{1}p_{2}\)
(２)
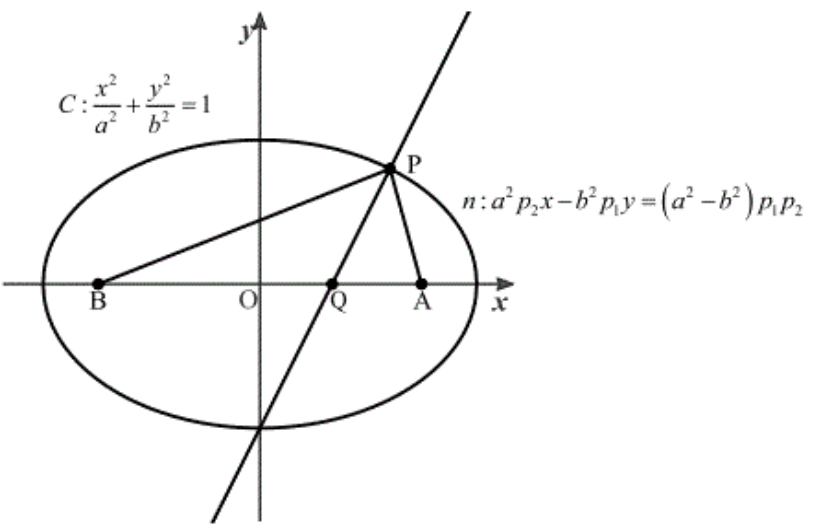
法線 \(n\) と \(x\) 軸の交点を \(Q\) とする．
(１)より，\(Q\left(\displaystyle\frac{a^2-b^2}{a^2}p_{1},0\right)\) となる．
ここで，線分 \(AP\)，\(BP\)，\(AQ\)，\(BQ\) について
\(AP^2=\left(\sqrt{a^2-b^2}-p_{1}\right)^2+p_{2}^2\)
\(=a^2-b^2-2\sqrt{a^2-b^2}p_{1}+p_{1}^2+p_{2}^2\)
\(\displaystyle\frac{p_{1}^2}{a^2}+\displaystyle\frac{p_{2}^2}{b^2}=1\)
\(\iff\) \(p_{2}^2=b^2-\displaystyle\frac{b^2p_{1}^2}{a^2}\) より
\(AP^2=\left(p_{1}^2-2\sqrt{a^2-b^2}p_{1}+a^2-b^2\right)+\left(b^2-\displaystyle\frac{b^2p_{1}^2}{a^2}\right)\)
\(=\displaystyle\frac{a^2-b^2}{a^2}p_{1}^2-2\sqrt{a^2-b^2}p_{1}+a^2\)
\(=\left(\displaystyle\frac{\sqrt{a^2-b^2}}{a}p_{1}-a\right)^2\)
よって，\(AP=a-\displaystyle\frac{\sqrt{a^2-b^2}}{a}p_{1}\) ( ∵\(p_{1}<a\) )
\(BP=2a-AP=a+\displaystyle\frac{\sqrt{a^2-b^2}}{a}p_{1}\)
\(AQ=\sqrt{a^2-b^2}-\displaystyle\frac{a^2-b^2}{a^2}p_{1}=\displaystyle\frac{\sqrt{a^2-b^2}}{a}AP\)
\(BQ=\sqrt{a^2-b^2}+\displaystyle\frac{a^2-b^2}{a^2}p_{1}=\displaystyle\frac{\sqrt{a^2-b^2}}{a}BP\)
ゆえに，\(AP：BP=AQ：BQ\) が成り立つので，法線 \(n\) は \(\angle APB\) の二等分線となる．
コメント