\(a , b\) は \(0\) でない整数とする.
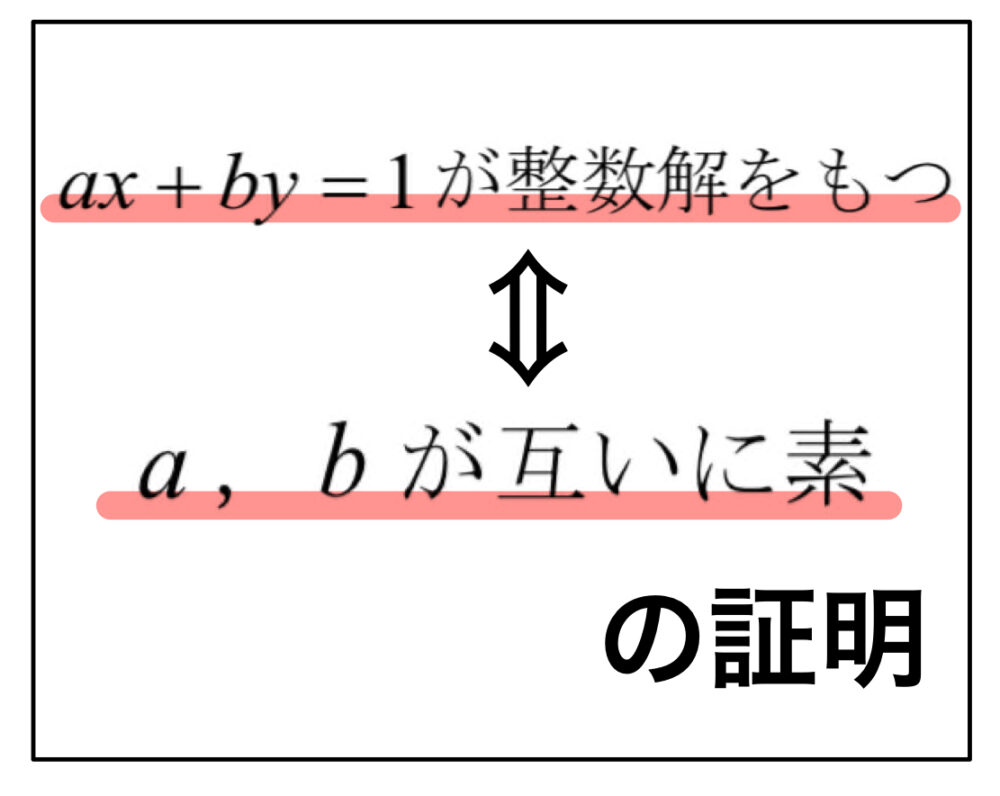
「\(ax+by=1\)が整数解をもつ」・・・①
「\(a , b\) が互いに素」・・・②
①と②が必要十分条件であることを証明せよ.
必要十分条件(同値)の証明の仕方について
必要十分条件(同値)については、大きく次の2つの証明の仕方があります。
【1】同値性を一度に示す
【2】「 ① ⇒ ② が真 」と「 ② ⇒ ① が真 」をそれぞれ示す
【1】については、①(または②)からスタートして、常に同値性を保ちながら式変形をしていき、②(または①)の形に持っていく.
【2】については、①からスタートして②、②からスタートして①をそれぞれ場合分けをして証明をする.
【1】に関しては、同値性が崩れていないかを気にしながら証明を与える必要があるため、数学的な力がより問われます.気がつかないうちに同値性が崩れていることがあるため、【1】で解答を作った場合、自分の中では満点だと思っていても、大幅に減点をされる可能性があります。
☆何気なく記述していて同値が崩れている例☆
・\(x=2\) より \(x^2=4\) なので・・・
「\(x=2\) ⇒ \(x^2=4\) は真」であるが、「\(x^2=4\) ⇒ \(x=2\) は偽」である.
【2】に関しては、同値性が崩れることを気にすることなく証明することができる点でメリットがあります.
【補題】証明のための準備
\(a , p\) が互いに素なとき、\(a , 2a , 3a , \cdots , (p-1)a\) を \(p\) で割った余りはすべて異なる
証明
\(ma\) と \(na\) \(( 1 ≦ m < n < p )\) を \(p\) で割った余りが等しいと仮定する.
つまり、
\(na-ma = (n-m)a\) は \(p\) の倍数・・・(※)
となるが、
\( 1 ≦ n-m < p\) かつ \(a , p\) は互いに素であるから、
\((n-m)a\) が \(p\) の倍数であることは矛盾.
したがって、
\(a , p\) が互いに素なとき、\(a , 2a , 3a , \cdots , (p-1)a\) を \(p\) で割った余りはすべて異なる
【参考】(※)について

「フェルマーの小定理の証明」の際にも利用した性質だね!
【証明】
\(a , b\) は \(0\) でない整数とする.
「\(ax+by=1\)が整数解をもつ」・・・①
「\(a , b\) が互いに素」・・・②
①と②が必要十分条件であることを証明せよ.
( ⅰ ) ① ⇒ ②について
対偶証明で考える.
① ⇒ ② の対偶をとり
「\(a , b\) が互いに素でない」⇒「\(ax+by=1\)が整数解をもたない」を示せば良い.
\(a , b\) が互いに素でないので、\(a , b\) の最大公約数を \(g ( ≧ 2 )\) とすると、
\(a=gA\) 、\(b=gB\)
(ただし \(A , B \) は互いに素な整数)
このとき、
\(ax+by=gAx+gBy=g(Ax+By)\) より、
\(Ax+By\) は整数で、 \(ax+by\) は \(g ( ≧ 2 )\) の倍数となり、
\(ax+by=1\) を満たす整数解をもたない
( ⅱ ) ② ⇒ ①について
【補題】より \(a , b\) が互いに素なとき、
\(a , 2a , 3a , \cdots , (b-1)a\) を \(b\) で割った余りはすべて異なるので、
余りが「 1 」となるものが存在する.
それを \(ma\)(\(1 ≦ m ≦ b-1\))とおき、\(b\) で割った商を \(n\) とおくと、
\(ma=bn+1\)
\(am+b(-n)=1\) となり
\(( x , y )=( m , -n )\) が整数解となる.
( ⅰ )、( ⅱ )より、①と②は必要十分条件である.
最後に(互いに素であることの証明)
この性質を用いることで次のようなことができます.
\(a=n , b=n+1\) として、
\(nx+(n+1)y=1\) を考えるとき、
\(( x , y )=( -1 , 1 )\) という整数解をもつので、
\(n , n+1\) は互いに素であることがわかる.
つまり、連続する 2 つの整数は互いに素である.
互いに素であることの証明の仕方については「2005 東京大学【整数問題】3 以上 999 以下の奇数 \(a\) で、\(a^2-a\) が 10000 で割り切れるもの」でも一部紹介をしています。






コメント
( ⅰ ) ① ⇒ ②についての証明について,
ax+by=a×gA+b×gB=g(aA+bB)
の部分は
ax+by=gA×x+gB×y=g(Ax+By)
ではないでしょうか?AもBも整数であるためAx+Byも整数となると思うのですがいかがでしょうか?
コメントありがとうございます。
ご指摘していただいた点ですが、誤りでした。
ご指摘いただき誠にありがとうございます。
訂正させていただきました。
今後ともよろしくお願いします。