【2021東北大学・文】
(1) \(3\) 次関数 \(y=x^3+x^2\) のグラフと \(2\) 次関数 \(y=x^2+4x+16\) のグラフの共通接線は \(2\) 本ある.それらの方程式を求めよ.
(2) (1)で求めた \(2\) 本の共通接線と \(2\) 次関数 \(y=x^2+4x+16\) のグラフで囲まれた部分の面積を求めよ.
(1)共通接線(共有点なし)の求め方・考え方
《解法の流れ》
[解法①]
一方の曲線に接点を与え、接線の方程式を求める.
その接線が、他方の曲線と接する条件を考える.
[解法②]
それぞれの曲線に接点を与え、それぞれ接線の方程式を求める.
その 2 接線が一致する条件を考える.
共通接線の解法については,共有点がある場合とない場合で異なります。
より詳しい考え方・例題は【数学Ⅱ・微分】共通接線2タイプの解法まとめ

(1) 解答①

解答①の流れは,主に数学Ⅱの範囲の問題(文系)で出題されることが多い!
また,過去のセンター試験でもこの誘導形式で出題されています!
\(f(x)=x^3+x^2\) , \(g(x)=x^2+4x+16\) とおく.
\(f^{\prime}(x)=3x^2+2x\) より,
\(x=t\) における接線の方程式は
\(y-f(t)=(3t^2+2t)(x-t)\)
\(y=(3t^2+2t)x-2t^3-t^2\) ・・・①
①が,\(y=g(x)\) と接するためには,
\(x^2+4x+16=(3t^2+2t)x-2t^3-t^2\)
\(\iff\) \(x^2-(3t^2+2t+4)x+2t^3+t^2+16=0\)
が重解をもてばよい.つまり判別式 \(D=0\) を満たせばよい.
\(D=(3t^2+2t+4)^2-4(2t^3+t^2+16)=0\)
\(\iff\) \(9t^4+4t^3-24t^2-16t-48=0\)
この式は,\(t=2 , -2\) を満たす(代入したら成立する)ので,
\((t-2)(t+2)(9t^2+4t+12)=0\) と因数分解できる.
よって,\(t=2,-2\) , \(9t^2+4t+12=0\)
\(9t^2+4t+12=0\) のとき,
\(t=\displaystyle\frac{-2\pm\sqrt{2^2-9\times 12}}{9}\) となり実数解とならないため不適.
したがって,\(t=2,-2\)
これらをそれぞれ①に代入すると,求める共通接線の方程式は
\(y=16x-20\) , \(y=8x+12\)
(1) 解答②

解答②の流れは,複雑な関数のとき(数学Ⅲでは必須の考え方)が多いです!
いずれも頻出ですので,しっかりと解けるように!
\(f(x)=x^3+x^2\) , \(g(x)=x^2+4x+16\) とおく.
\(f^{\prime}(x)=3x^2+2x\) より,
\(x=t\) における接線の方程式は
\(y-f(t)=(3t^2+2t)(x-t)\)
\(y=(3t^2+2t)x-2t^3-t^2\) ・・・①

ここまでは上の解答①と全く同じ。
次に \(x=s\) における \(y=g(x)\) の接線を求めよう!
次に,\(g(x)=x^2+4x+16\) において
\(g^{\prime}(x)=2x+4\) より,
\(x=s\) における接線の方程式は
\(y-g(s)=(2s+4)(x-s)\)
\(y=(2s+4)x-s^2+16\) ・・・②
①と②が一致するとき,\(y=f(x)\) と \(y=g(x)\) の共通接線となるので,
\(\begin{cases}3t^2+2t=2s+4 ・・・③\\-2t^3-t^2=-s^2+16 ・・・④\end{cases}\)
③より \(s=\displaystyle\frac{1}{2}(3t^2+2t-4)\) を④に代入して式を整理すると,
\(9t^4+4t^3-24t^2-16t-48=0\)

以下,省略。
ここからは解答①と全く同じです。
(2)2接線と放物線で囲まれた図形の面積
(1)の結果から(2)の問題は
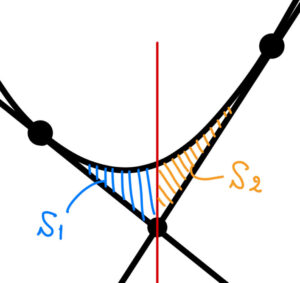 ※ 右図はあくまでもイメージ(正確な位置関係のグラフではありません)
※ 右図はあくまでもイメージ(正確な位置関係のグラフではありません)
まず初めに,それぞれのグラフの交点の \(x\) 座標を調べる.
( ⅰ ) \(y=16x-20\) , \(y=8x+12\) の交点の \(x\) 座標は \(x=4\)
( ⅱ ) \(y=8x+12\) , \(y=x^2+4x+16\) の交点の \(x\) 座標は
\(x^2+4x+16=8x+12\)
\((x-2)^2=0\)
よって \(x=2\)
( ⅲ ) \(y=16x-20\) , \(y=x^2+4x+16\) の交点の \(x\) 座標は
\(x^2+4x+16=16x-20\)
\((x-6)^2=0\)
よって \(x=6\)
したがって,
\(S_{1}=\displaystyle\int ^4_2\left\{(x^2+4x+16)-(8x+12)\right\}\enspace dx\)
\(=\displaystyle\int ^4_2{(x-2)^2}\enspace dx\)
\(=\Bigl[\displaystyle\frac{1}{3}(x-2)^3\Bigr]^{4}_{2}=\displaystyle\frac{8}{3}\)
また,
\(S_{2}=\displaystyle\int ^6_4\left\{(x^2+4x+16)-(16x-20)\right\}\enspace dx\)
\(=\displaystyle\int ^6_4{(x-6)^2}\enspace dx\)
\(=\Bigl[\displaystyle\frac{1}{3}(x-6)^3\Bigr]^{6}_{4}=\displaystyle\frac{8}{3}\)
したがって,求める面積は \(\displaystyle\frac{8}{3}+\displaystyle\frac{8}{3}=\displaystyle\frac{16}{3}\)
参考:共通テスト裏技公式!
(2)について覚えておいてほしい裏技公式
《注意》以下は記述の解答では使用できません!
下図のような放物線の2接線の交点の \(x\) 座標について
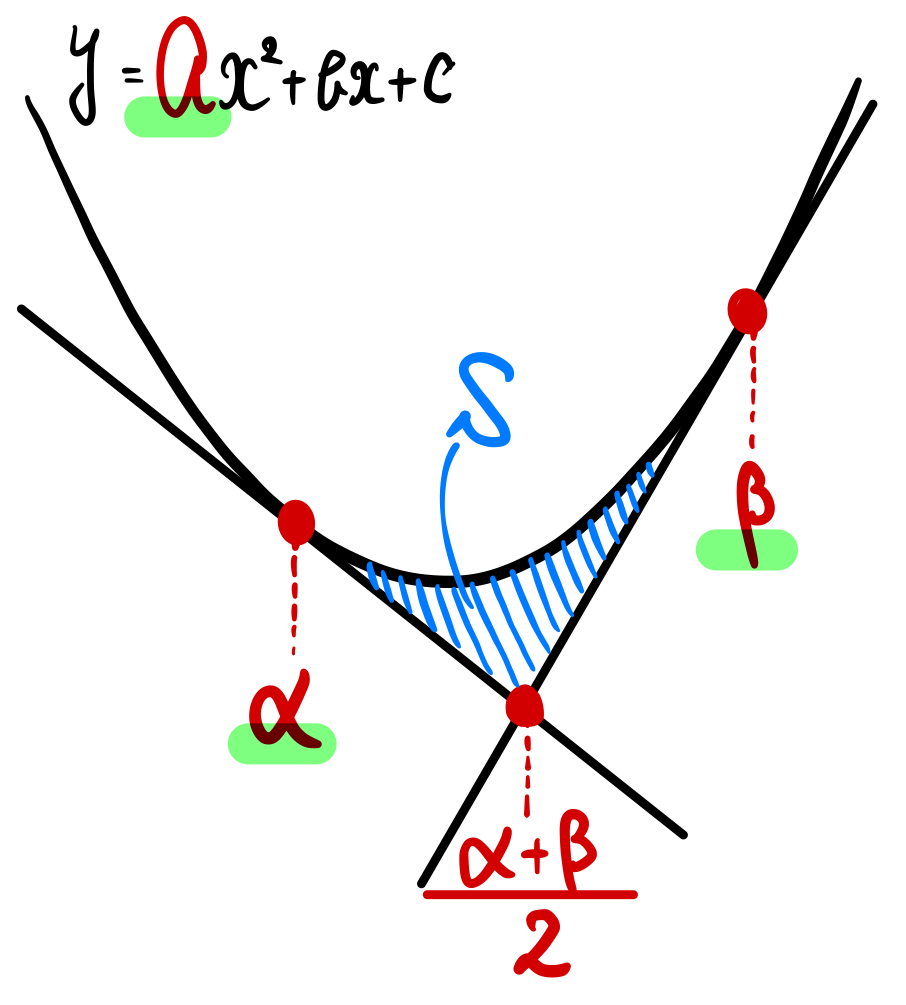
・2 接点を \(x=\alpha\),\(\beta\) のとき、2 接線の交点の \(x\) 座標は各接点の”中点”になる
・放物線と 2 接線で囲まれた面積は、\(S=\displaystyle\frac{a}{12}(\beta-\alpha)^3\)
(※ \(a\) は放物線の 2 乗の係数)
・面積 \(S\) は \(x=\displaystyle\frac{\alpha+\beta}{2}\) で 2 等分される








コメント