【2022兵庫県立大学・社会情報】(4/9)<(n/m)<(1/2)を満たす自然数の組でmの最小

【2022兵庫県立大学・社会情報科・第１問( Ⅰ )】

不等式 \(\displaystyle\frac{4}{9}<\displaystyle\frac{n}{m}<\displaystyle\frac{1}{2}\) を満たす自然数の組 \((m,n)\) のうち \(m\) の最小である組 \((m_{0},n_{0})\) を求めなさい．

考え方・方針について
解答・解説
補足：加比の理

考え方・方針について

「整数問題」の極意は実験！

本問は最小の \(m\) を求めたいので，まずは \(m\) について解き， \(n\) に具体的な値を代入して具体的に実験してみましょう！

\(\displaystyle\frac{4}{9}<\displaystyle\frac{n}{m}<\displaystyle\frac{1}{2}\) を \(m\) について解くと

\(2n<m<\displaystyle\frac{9}{4}n\) ・・・①

・\(n=1\) のとき

① \(\iff\) \(2<m<\displaystyle\frac{9}{4}\) となり

これを満たす自然数 \(m\) は存在しない．

上のように，\(n=2,3,4,\cdots\) と具体的に実験していけば，最小となる値がわかりますね！

解答・解説

\(\displaystyle\frac{4}{9}<\displaystyle\frac{n}{m}<\displaystyle\frac{1}{2}\) を \(m\) について解くと

\(2n<m<\displaystyle\frac{9}{4}n\) ・・・①

・\(n=1\) のとき

① \(\iff\) \(2<m<\displaystyle\frac{9}{4}\) となり

これを満たす自然数 \(m\) は存在しない．

・\(n=2\) のとき

① \(\iff\) \(4<m<\displaystyle\frac{9}{2}\) となり

これを満たす自然数 \(m\) は存在しない．

・\(n=3\) のとき

① \(\iff\) \(6<m<\displaystyle\frac{27}{4}\) となり

これを満たす自然数 \(m\) は存在しない．

・\(n=4\) のとき

① \(\iff\) \(8<m<9\) となり

これを満たす自然数 \(m\) は存在しない．

・\(n=5\) のとき

① \(\iff\) \(10<m<\displaystyle\frac{45}{4}\) となり

これを満たす自然数 \(m=11\)

・\(n≧6\) のとき

① \(\iff\) \(12≦2n<m<\displaystyle\frac{9}{4}n\) より，\(m>11\)

ゆえに①を満たす最小の \(m=11\)

したがって，\((m_{0},n_{0})=(11,5)\)

補足：加比の理

加比の理

① 等式タイプ

\(\displaystyle\frac{b}{a}=\displaystyle\frac{d}{c}\) のとき，\(\displaystyle\frac{b}{a}=\displaystyle\frac{d}{c}=\displaystyle\frac{b+d}{a+c}\)

② 不等式タイプ

\(\displaystyle\frac{b}{a}<\displaystyle\frac{d}{c}\) のとき，\(\displaystyle\frac{b}{a}<\displaystyle\frac{b+d}{a+c}<\displaystyle\frac{d}{c}\)

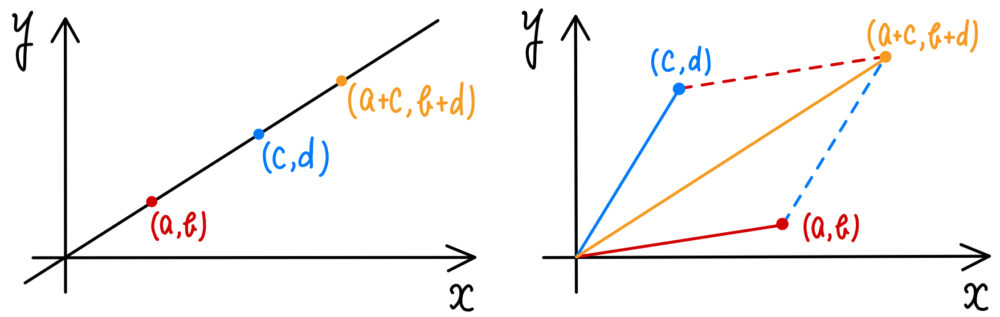
ここでは厳密な証明は省略しますが，下図の”傾き”に注目すると，加比の理が成り立つのは明らかですね！

本問では， \(\displaystyle\frac{4}{9}<\displaystyle\frac{1}{2}\) より， \(\displaystyle\frac{4}{9}<\displaystyle\frac{5}{11}<\displaystyle\frac{1}{2}\) が成り立つので，\((m,n)=(11,5)\) は答えの \(1\) つであることは分かります！