【2019徳島大学ー医歯薬】
自然数 \(n\) に対して、\(f(n)=n^2(n^2+8)\) と定める.
\(f(n)\) の正の約数の個数が \(10\) 個であるような \(n\) をすべて求めよ.
考え方・方針の立て方
正の約数の個数について
自然数 \(N\) が \(N=a^x b^y c^z \cdots\) と素因数分解できるとき、
\(N\) の正の約数の個数は、\((x+1)(y+1)(z+1)\cdots\) となる.
このことから、正の約数の個数が \(10\) 個のとき、異なる素数 \(p\)、\(q\) を用いて、
\(p^9\) または \(p^4\times q\) の形のいずれかになる.
平方数・指数はmod 3,4,5,8 が有効
難関大学ではよく出題されるPointの1つ!
まずは下の表を見てください。
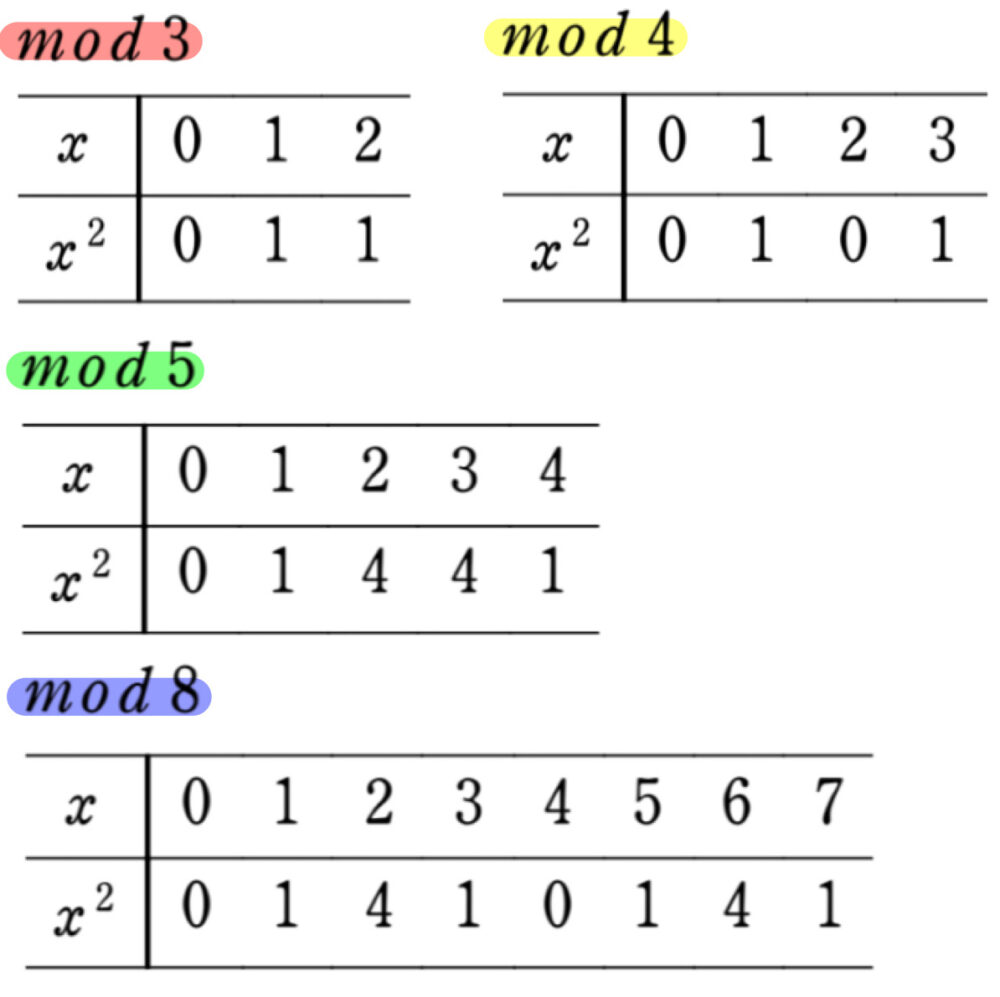
- mod 3 ➡ 「0、1」のみ
- mod 4 ➡ 「0、1」のみ
- mod 5 ➡ 「0、1、4」のみ
- mod 8 ➡ 「0、1、4」のみ
この性質を使って解く演習問題



ここで、\(mod 3\) として考えると、
・\(n≡0\) のとき、\(n^2≡0\)、\(n^2+8≡2\)
・\(n≡\pm1\) のとき、\(n^2≡1\)、\(n^2+8≡0\)
であるから、\(n^2\) と \(n^2+8\) のいずれか一方は \(3\) の倍数で、もう一方は \(3\) の倍数とならない.
\(f(n)\) は少なくとも \(3\) を約数に持つことが分かったので、
\(f(n)=\)\(3^9\) または \(3^4\times q\) または \(p^4\times 3\) の形のいずれか
解答
【2019徳島大学ー医歯薬】
自然数 \(n\) に対して、\(f(n)=n^2(n^2+8)\) と定める.
\(f(n)\) の正の約数の個数が \(10\) 個であるような \(n\) をすべて求めよ.
\(mod 3\) として考えると、
・\(n≡0\) のとき、\(n^2≡0\)、\(n^2+8≡2\)
・\(n≡\pm1\) のとき、\(n^2≡1\)、\(n^2+8≡0\)
であるから、\(n^2\) と \(n^2+8\) のいずれか一方は \(3\) の倍数で、もう一方は \(3\) の倍数とならない・・・①
\(f(n)\) の正の約数の個数が \(10\) 個であるから、異なる素数 \(p\)、\(q\) を用いて、
\(f(n)=\)\(3^9\) または \(3^4\times q\) または \(p^4\times 3\) の形のいずれか.
(ア) \(f(n)=\)\(3^9\) のとき
\(n^2<n^2+8\) かつ ① より
\(\begin{cases}n^2=1\\n^2+8=3^9 \end{cases}\)
しかしこの \(2\) 式を同時に満たす自然数 \(n\) は存在しないため不適
(イ) \(f(n)=\)\(3^4\times q\) のとき
\(n^2<n^2+8\) かつ ① かつ \(n^2\)(平方数) であることに注意すると、
(ⅰ) \(\begin{cases}n^2=1\\n^2+8=3^4\times q \end{cases}\) のとき
これを解くと、\(n=1\)、\(q=\displaystyle\frac{1}{9}\) となり、\(q\) が素数であることに反する.
(ⅱ) \(\begin{cases}n^2=3^4\\n^2+8=q \end{cases}\) のとき
これを解くと、\(n=9\)、\(q=89\) となり条件に適する.
(ウ) \(f(n)=\)\(p^4\times 3\) のとき
\(n^2<n^2+8\) かつ ① かつ \(n^2\)(平方数) であることに注意すると、
(ⅰ) \(\begin{cases}n^2=1\\n^2+8=p^4\times 3 \end{cases}\) のとき
これを解くと、\(n=1\)、\(p^4=3\) となり、これを満たす自然数 \(p\) が存在しない.
(ⅱ) \(\begin{cases}n^2=p^2\\n^2+8=p^2\times 3 \end{cases}\) のとき
これを解くと、\(p=n=2\) となり条件に適する.
(ⅲ) \(\begin{cases}n^2=p^4\\n^2+8=3 \end{cases}\) のとき
これを解くと、\(n^2=-5\) となりこれを満たす自然数は存在しないため不適.
したがって、求める \(n= 2 , 9\)







コメント