【2023神戸大学・文系・第3問】
\(a\) を正の実数とする.\(2\) つの円
\(C_{1}\):\(x^2+y^2=a\) ,\(C_{2}\):\(x^2+y^2-6x-4y+3=0\)
が異なる \(2\) 点 \(A\) , \(B\) で交わっているとする.直線 \(AB\) が \(x\) 軸および \(y\) 軸と交わる点をそれぞれ \((p,0)\) ,\((0,q)\) とするとき,以下の問に答えよ.
(1) \(a\) のとりうる値の範囲を求めよ.
(2) \(p\),\(q\) の値を \(a\) を用いて表せ.
(3) \(p\),\(q\) の値が共に整数となるような \(a\) の値をすべて求めよ.
解答・解説
(1) \(a\) のとりうる値の範囲

\(2\) 円が異なる \(2\) 点で交わるとき
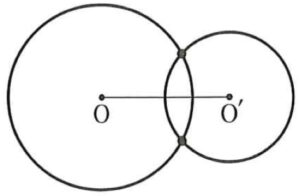
\(r-r^{\prime}<d<r+r^{\prime}\)
(※\(d\) は中心間距離)

\(C_{1}\):\(x^2+y^2=a\)
\(C_{2}\):\((x-3)^2+(y-2)^2=10\)
\(C_{1}\) は中心が \((0,0)\),半径が \(\sqrt{a}\)
\(C_{2}\) は中心が \((3,2)\),半径が \(\sqrt{10}\) の円で
\(2\) 円の中心間距離は \(\sqrt{3^2+2^2}=\sqrt{13}\)
よって,\(2\) つの円が異なる \(2\) 点で交わるとき
\(\sqrt{13}-\sqrt{10}<\sqrt{a}<\sqrt{13}+\sqrt{10}\)
\(23-2\sqrt{130}<a<23+2\sqrt{130}\)
(2) \(p\),\(q\) の値を \(a\) を用いて表せ.
\(2\) つの曲線の交点を通る曲線
\(2\) つの曲線 \(f(x,y)=0\),\(g(x,y)=0\) に対して,
\(f(x,y)+kg(x,y)=0\)
は \(2\) つの曲線の交点を通る曲線を表す
\(C_{1}\) と \(C_{2}\) の交点を通る図形の方程式は
\((x^2+y^2-a)+k(x^2+y^2-6x-4y+3)=0\)
これが \(2\) 円の交点を通る直線となるのは,\(k=-1\) のとき
よって直線 \(AB\) は
\(6x+4y-a-3=0\)
\(y=0\) のとき \(x=\displaystyle\frac{a+3}{6}\)
\(x=0\) のとき \(y=\displaystyle\frac{a+3}{4}\)
よって,\(p=\displaystyle\frac{a+3}{6}\),\(q=\displaystyle\frac{a+3}{4}\)
(3) \(p\),\(q\) の値が共に整数となるような \(a\) の値
(2) より
\(a+3=6p=4q\) ・・・①
よって,\(3p=2q\)
\(2\) と \(3\) は互いに素であるから,整数 \(m\) を用いて
\(p=2m\) ,\(q=3m\) とおける.
①より \(a+3=12m\) \(\iff\) \(a=12m-3\)
(1) より
\(23-2\sqrt{130}<12m-3<23+2\sqrt{130}\)
\(\displaystyle\frac{13-\sqrt{130}}{6}<m<\displaystyle\frac{13+\sqrt{130}}{6}\)
\(11<\sqrt{130}<12\) で \(m\) は整数より
\(m=1,2,3,4\)
したがって,\(a=9,21,33,45\)








コメント