【2024京都大学・文系・第３問】絶対値を含む２次関数の最大値の場合分け

【2024京都大学・文系・第３問】

\(a\) は正の定数とする．次の関数の最大値を求めよ．

\(f(x)=\left|x^2-\left(ax+\displaystyle\frac{3}{4}a^2\right)\right|+ax+\displaystyle\frac{3}{4}a^2\)　\(\left(-1≦x≦1\right)\)

解答・解説

\(x^2-\left(ax+\displaystyle\frac{3}{4}a^2\right)=\left(x+\displaystyle\frac{1}{2}a\right)\left(x-\displaystyle\frac{3}{2}a\right)\) より

(ⅰ)　\( x^2-\left(ax+\displaystyle\frac{3}{4}a^2\right)≧0\) \(\iff\) \(x≦-\displaystyle\frac{1}{2}a,\displaystyle\frac{3}{2}a≦x\) のとき

\(f(x)=x^2-\left(ax+\displaystyle\frac{3}{4}a^2\right)+ax+\displaystyle\frac{3}{4}a^2\)

\(f(x)=x^2\)

(ⅱ)　\( x^2-\left(ax+\displaystyle\frac{3}{4}a^2\right)<0\) \(\iff\) \(-\displaystyle\frac{1}{2}a<x<\displaystyle\frac{3}{2}a\) のとき

\(f(x)=- \left\{x^2-\left(ax+\displaystyle\frac{3}{4}a^2\right) \right\}+ax+\displaystyle\frac{3}{4}a^2\)

\(f(x)=-x^2+2ax+\displaystyle\frac{3}{2}a^2\) となるので

\(f(x)=-(x-a)^2+\displaystyle\frac{5}{2}a^2\)

ここで，\(y=\displaystyle\frac{5}{2}a^2\) となる \(x\) の値を考えると

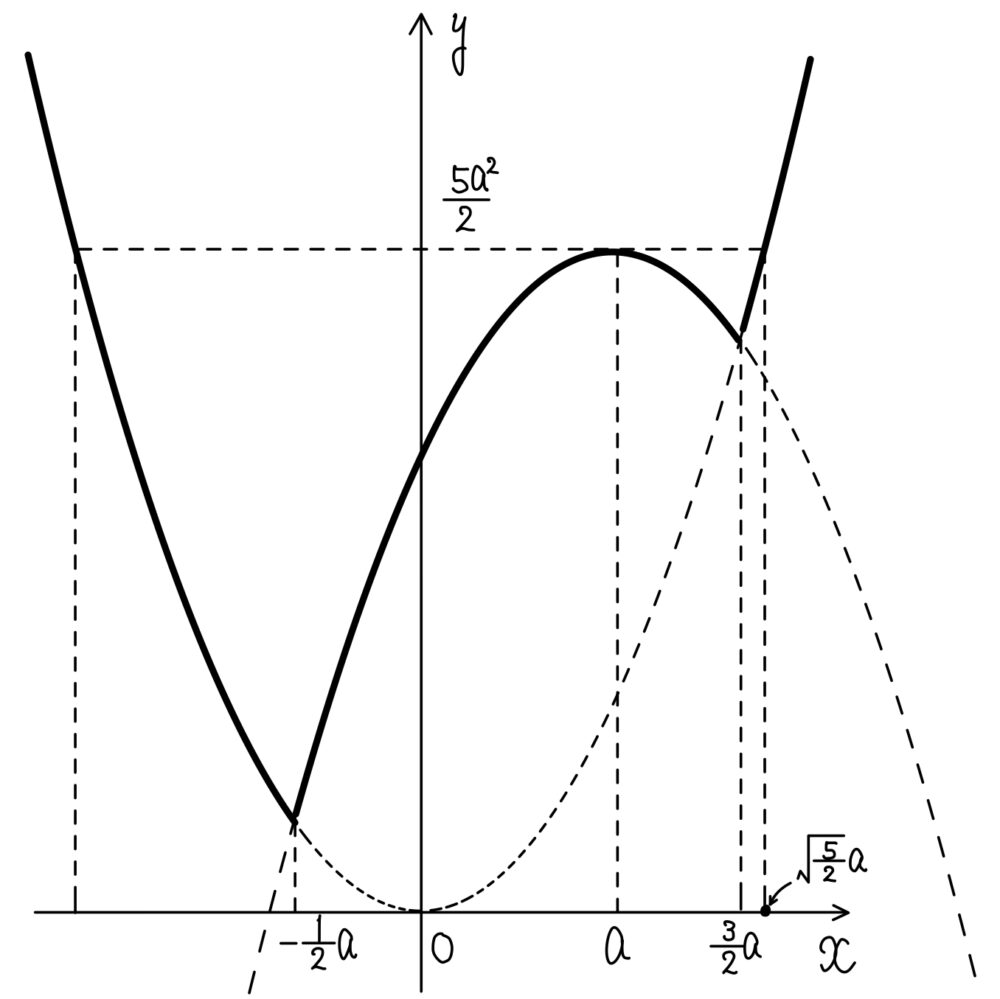(ⅰ)のとき

\(x^2=\displaystyle\frac{5}{2}a^2\) \(\iff\) \(x=\pm\sqrt{\displaystyle\frac{5}{2}}a\)

よって(ⅰ)，(ⅱ)から \(y=f(x)\) のグラフは右図のようになる．

\(-1≦x≦1\) における最大値は

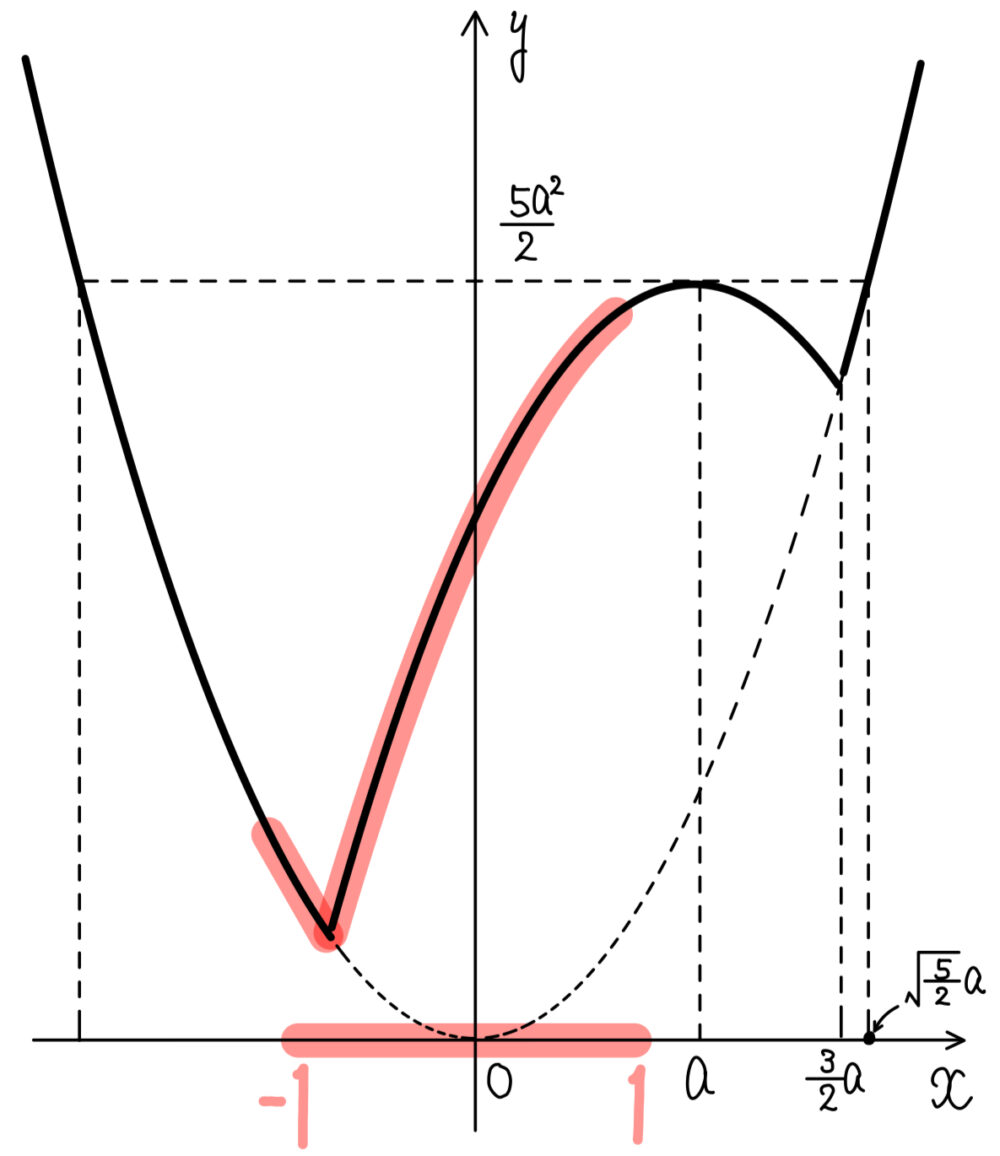(ア)　\(1<a\) のとき

\(x=1\) で最大値：\(\displaystyle\frac{3}{2}a^2+2a-1\)

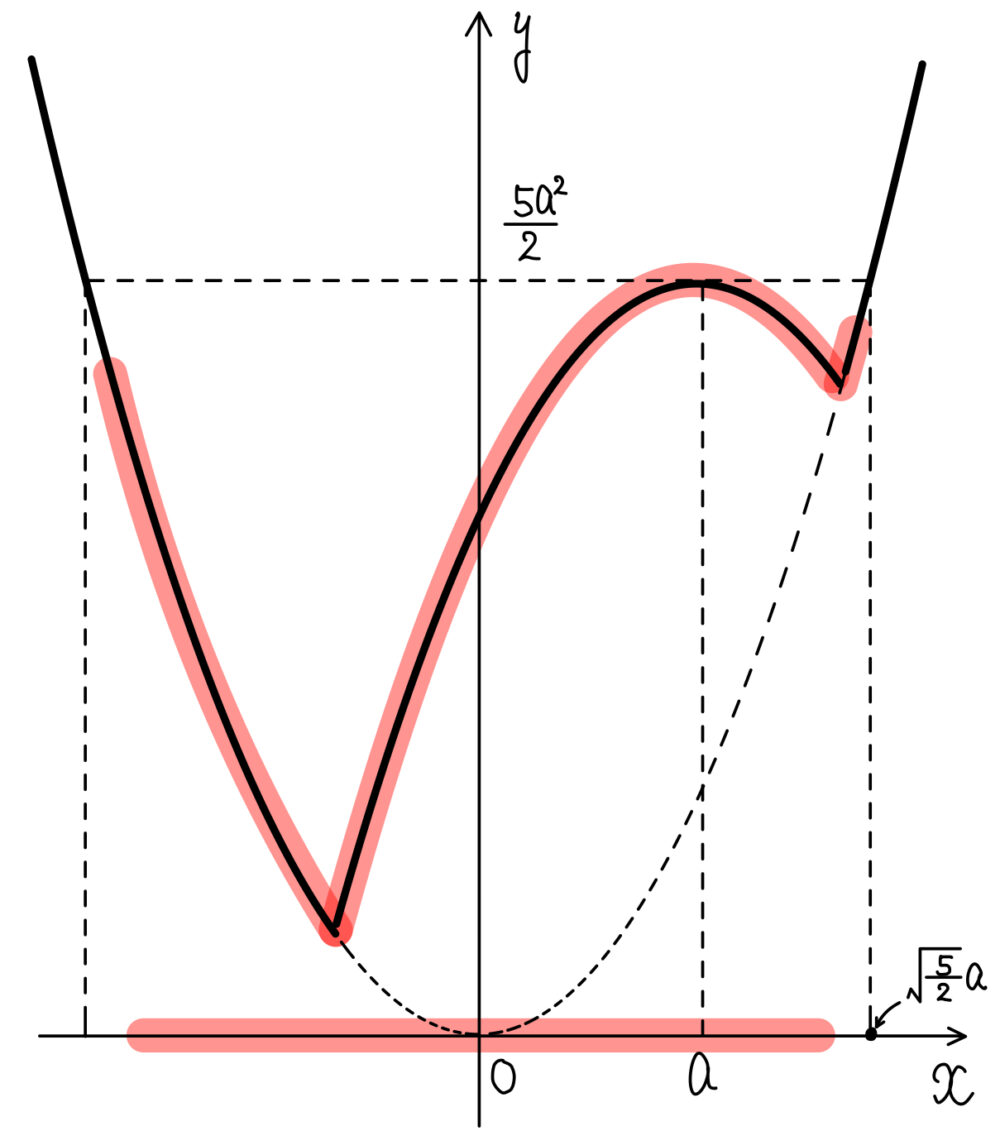(イ)　\(a≦1≦\sqrt{\displaystyle\frac{5}{2}}a \) \(\iff\) \(\displaystyle\frac{\sqrt{10}}{2}≦a≦1\) のとき

\(x=a\) で最大値：\(\displaystyle\frac{5}{2}a^2\)

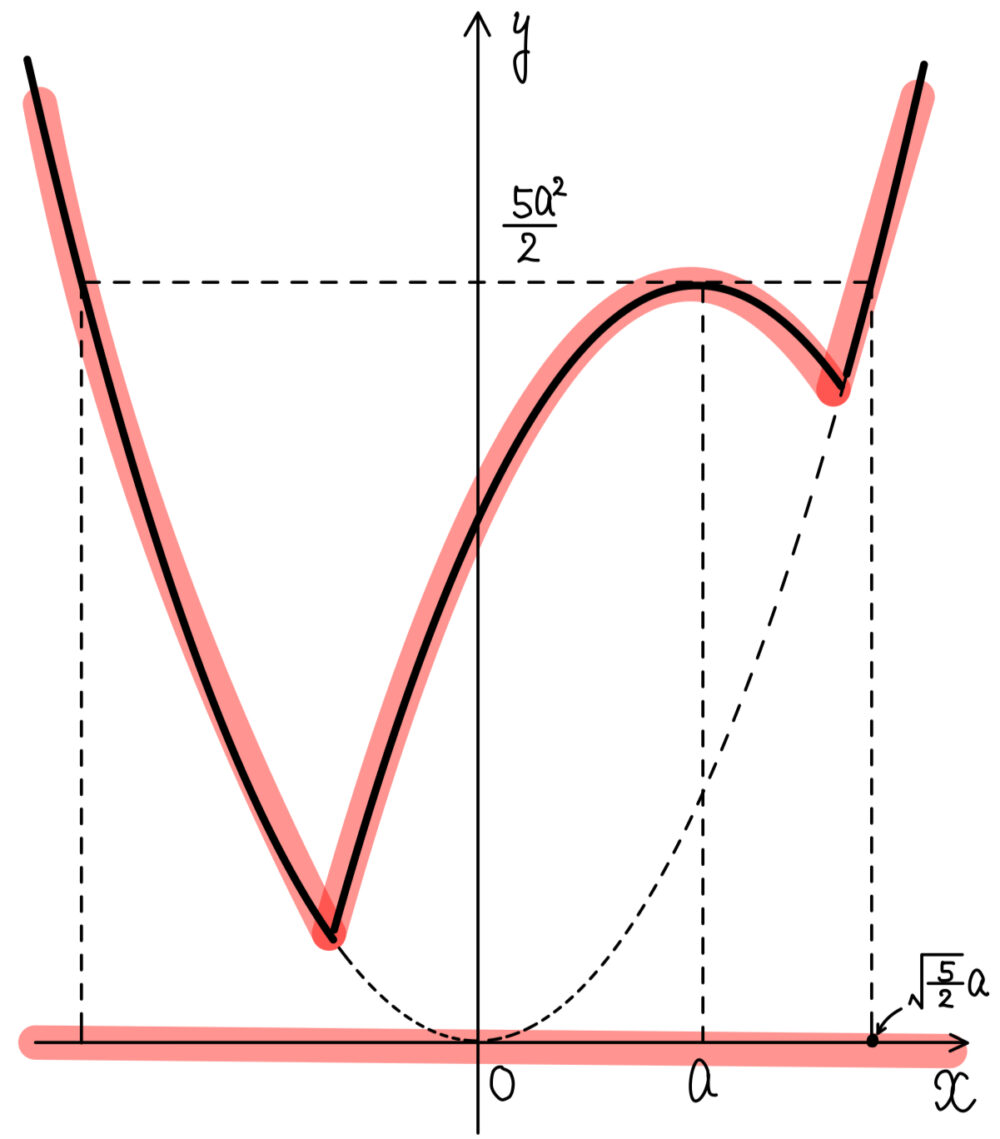(ウ)　\(\sqrt{\displaystyle\frac{5}{2}}a≦1\) \(\iff\) \(a≦\displaystyle\frac{\sqrt{10}}{2}\) のとき

\(x=\pm 1\) で最大値：\(1\)