さいころの目a , b , cを 3 辺の長さとする鋭角三角形ができる確率

三角形の成立条件

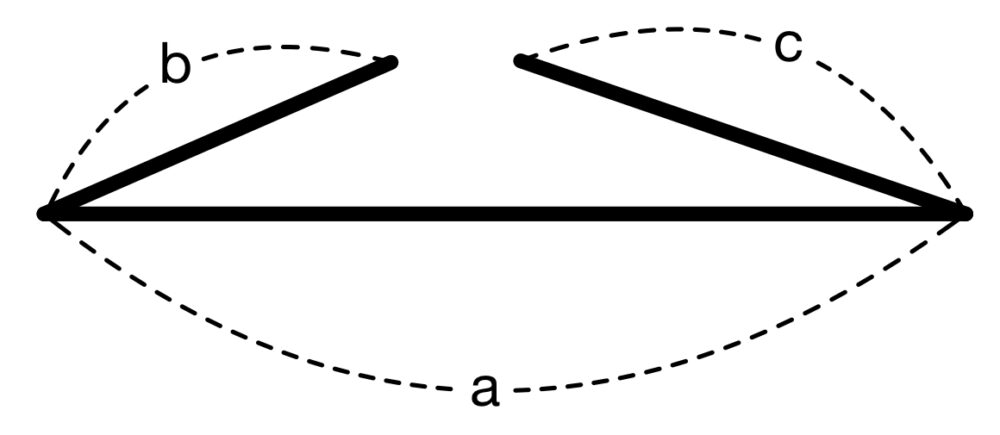
上の図のように、

\(b+c<a\) のとき( 2 辺を足しても辺 \(a\) に届かない)

三角形は当然ながら存在しない．

つまり、三角形が存在するためには

\(\begin{cases}a<b+c\\b<c+a\\c<a+b\end{cases}\)

つまり、

\(\begin{cases}a-b<c\\b-a<c\\c<a+b \end{cases}\)

これを 1 つにまとめて、

\(|a-b|<c<a+b\)

（１）解答

\(a , b , c\) を 3 辺の長さとする三角形が出来る条件は、

\(|a-b|<c<a+b\) ・・・①

サイコロを振って 1、2 回目に出る目 \(( a , b )\) の数に応じ、

①を満たす \(c\) の目を、下の表に表すと、

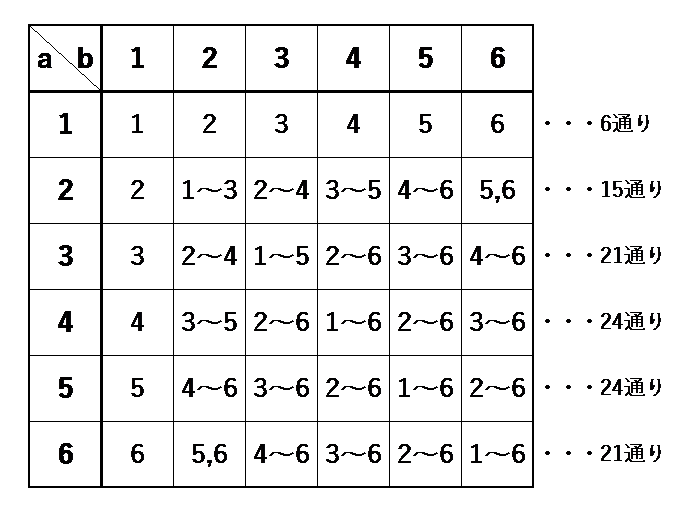
上の表より、①を満たすのは、

\(6+15+21+24+24+21=111\)

\(\displaystyle{\frac{111}{6^3}=\frac{37}{72}}\)

（１）の別解

普通にカウントしていくとなかなか大変・・・

先ほどは、正攻法（そのまま）で考えてみたが、それなりに大変であった．

よって2つ目の解法である「余事象」で考えてみる．

余事象を利用した（１）の別解

三角形ができないのは、

(ⅰ)　\(a+b≦c\)

(ⅱ)　\(b+c≦a\)

(ⅲ)　\(c+a≦b\) のとき

(ⅰ)について

・\(c=1\) のとき

\(a+b≦1\) を満たす \(( a , b )\) は存在しない

・\(c=2\) のとき

\(a+b≦2\) を満たす \(( a , b ) は

\(( a , b )=( 1 , 1 )\) の 1 通り

・\(c=3\) のとき

\(a+b≦3\) を満たす \(( a , b ) は

\(( a , b )=( 1 , 1 )、( 1 , 2 )、( 2 , 1 )\) の 3 通り

・\(c=4\) のとき

\(a+b≦4\) を満たす \(( a , b ) は

\(c=3\) のときを満たす 3 通りと、

\(( a , b )=( 1 , 3 )、( 2 , 2 )、( 3 , 1 )\) の 3 通り

よって、計 6 通り

・\(c=5\) のとき

\(a+b≦5\) を満たす \(( a , b ) は

\(c=4\) のときを満たす 6 通りと、

\(( a , b )=( 1 , 4 )、( 2 , 3 )、( 3 , 2 )、( 4 , 1 )\) の 4 通り

よって、計 10 通り

・\(c=6\) のとき

\(a+b≦6\) を満たす \(( a , b ) は

\(c=5\) のときを満たす 10 通りと、

\(( a , b )=( 1 , 5 )、( 2 , 4 )、( 3 , 3 )、( 4 , 2 )、( 5 , 1 )\) の 5 通り

よって、計 15 通り

以上から、

\(1+3+6+10+15=35\) 通り

(ⅱ)、(ⅲ)についても(ⅰ)と同様であるから、

求める確率は、

\(1-\displaystyle\frac{35\times3}{6^3}=\displaystyle\frac{37}{72}\)

どちらの解法が優れているかどうかではありません！

重要なのは両方考えられるようになること！

(2)解答

鋭角三角形ができる条件について

鋭角三角形

→ \(0<\angle{A}<90\text{°})\ かつ \(0<\angle{B}<90\text{°})\ かつ \(0<\angle{C}<90\text{°})\

→ \(\cos A>0\) かつ \(\cos B>0\) かつ \(\cos C>0\)

余弦定理から、

\(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}\) より、

→ \(\cos A=\displaystyle\frac{b^2+c^2-a^2}{2bc}>0\)

\(2bc>0\) より

\( b^2+c^2-a^2>0\)

同様に \(\cos B\)、\(\cos C\) について考えると、

\( c^2+a^2-b^2>0\)

\( a^2+b^2-c^2>0\)

よって、

\(|a^2-b^2|<c^2<a^2+b^2\)

(1)と同様に表にまとめると、

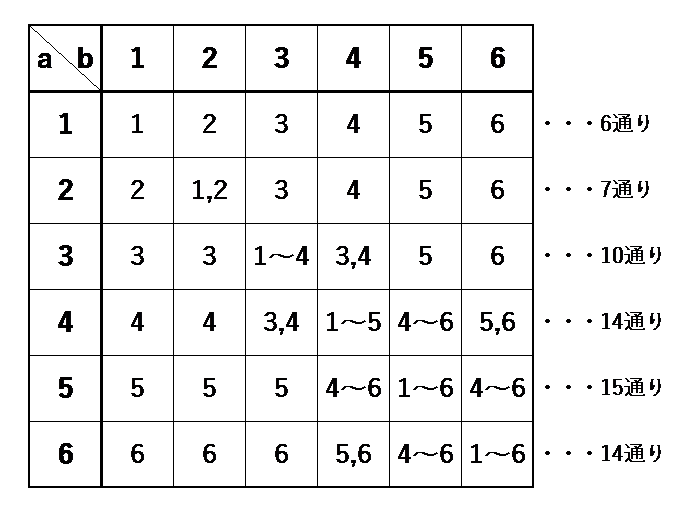
上の表から、

\(6+7+10+14+15+14=66\)

\(\displaystyle{\frac{66}{6^3}=\frac{11}{36}}\)