【2009京都大学】pのn乗の階乗 は p で何回割り切れるか[整数・ガウス記号・頻出]

考え方：具体的に実験！

実験①：\(p=2\)、\(n=3\) のとき

\(p=2\)、\(n=3\) として考えてみましょう．

このとき、「\((2^3)!=8!\) は \(2\) で何回割り切れるか」を考えればよいと言うことになります．

もちろん \(8!\) ぐらいであればゴリゴリと計算すれば答えは出せるが、それでは意味がありません．

どのような値になっても答えが作れるような解法(一般化できる解法)を以下のように考えていきます．

まず下の画像を見て下さい．

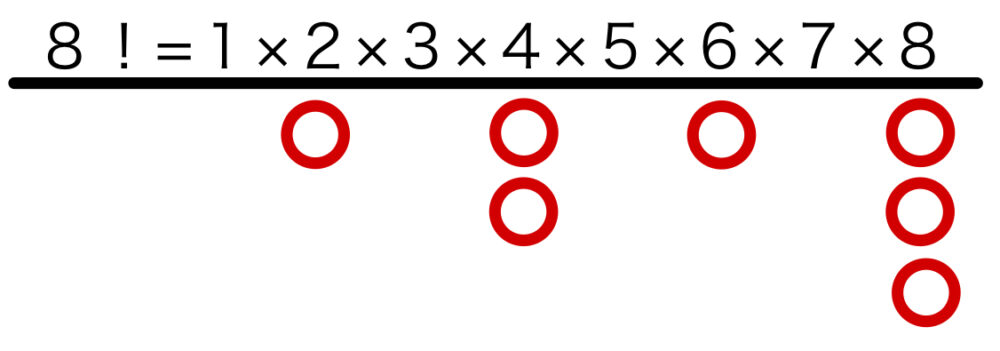
\(8!\) を積の形になおし、数字の下に○を付けました．

この○が表す意味は、\(2\) を約数に何個持つかを表しています．

例えば

・\(8=2^3\) であるから、\(2\) が \(3\) 個ある．それを○○○と表した．

・\(7\) であれば、\(2\) を約数に持たないため、○は書いていない．

このとき、

「\((2^3)!=8!\) は \(2\) で何回割り切れるか」と言う問は、

「○が全部で何個あるか？」という問と同じです．

つまり、○の個数を数えればよいわけであるが、この○の数え方が重要！！

これをただただ数えるだけでは、数が大きくなった時に、限界がきます．

そこで、次の画像を見て下さい．

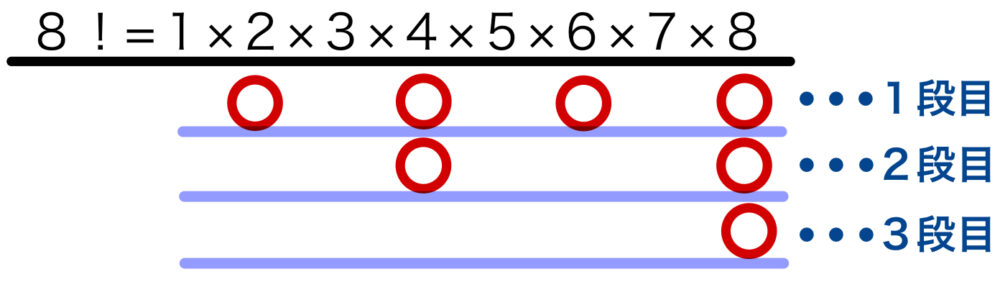
○のカウントの仕方は、横に何個ずつあるか、段ごとでカウントしていきます．

その理由としては、

\(1\) 段目については必ず \(2\) つ置きに○が現れます．

\(2\) 段目については必ず \(2^2=4\) つ置きに○が現れます．

\(3\) 段目については必ず \(2^3=8\) つ置きに○が現れます．

つまり、

\(1\) 段目の○の個数は、\(8\div 2 = 4\) 個

\(2\) 段目の○の個数は、\(8\div 2^2 = 2\) 個

\(3\) 段目の○の個数は、\(8\div 2^3 = 1\) 個

と計算を用いてカウントすることが出来ます．

よって、\(4+2+1=7\)

実験②：\(p=3\)、\(n=5\) のとき

もう少し大きな値で具体的に実験してみます．

\(p=3\)、\(n=5\) とする．

つまり、「\((3^5)!=243!\) は \(3\) で何回割り切れるか」を考えればよい．

\(1\) 段目の○の個数は、\(243\div 3 = 81\) 個

\(2\) 段目の○の個数は、\(243\div 3^2 = 27\) 個

\(3\) 段目の○の個数は、\(243\div 3^3 = 9\) 個

\(4\) 段目の○の個数は、\(243\div 3^4 = 3\) 個

\(5\) 段目の○の個数は、\(243\div 3^5 = 1\) 個

よって、\(81+27+9+3+1=121\) 個

※この方法を用いれば、数が大きくなっても(文字になっても)同様に扱うことが出来ます．

解答

\(1\) から \(p^n\) までの \(p^n\) 個の数のうち、

\(p\) で割り切れる数は、\(p^n\div p = p^{n-1}\) 個

\(p^2\) で割り切れる数は、\(p^n\div p^2 = p^{n-2}\) 個

\(p^3\) で割り切れる数は、\(p^n\div p^3 = p^{n-3}\) 個

・・・・（これを繰り返す）

\(p^{n-1}\) で割り切れる数は、\(p^n\div p^{n-1} = p\) 個

\(p^n\) で割り切れる数は、\(p^n\div p^n = 1\) 個

したがって、\((p^n)!\) は \(p\) で

\(p^{n-1}+ p^{n-2}+ p^{n-3}+\cdots+p+1=\displaystyle\frac{p^n-1}{p-1}\) (回)割り切れる．

補足：ガウス記号について

今回の問題はすべて綺麗に割り切れたため、特に気にすることがなかったのですが、

例えば、「\(10 !\) は \(2\) で何回割り切れるか」という問題を考えてみます．

基本的な考え方は同じなのですが、

\(1\) 段目は、\(10\div 2 = 5\) 　よって \(5\) 個

\(2\) 段目は、\(10\div 2^2 = 2.5\) となるため、整数部分の \(2\) 個となる．

\(3\) 段目は、\(10\div 2^3 = 1.25\) となるため、整数部分の \(1\) 個となる．

このように、割り切れない場合、整数部分を考えればよいが、これをガウス記号を用いて

\(\displaystyle\left[\frac{10}{2}\right]+\displaystyle\left[\frac{10}{2^2}\right]+\displaystyle\left[\frac{10}{2^3}\right]=5+2+1=8\) と書ける．