2次関数は、高校数学の内容において最も重要な分野の1つです。
そして、高校数学が出来る出来ないの分岐点になるのも2次関数。
その中でも特に、最大値・最小値の場合分けの問題は差がつき始める問題の1つ。
そこでしっかりと場合分けのパターンに慣れ、最初の関門を突破しましょう!
ここでは、「軸が動くタイプ」「範囲の両端が動くタイプ」についてのパターン化です。
まず初めに、
2次関数の最大値・最小値の問題
👉 ① 凸方向の確認
👉 ② 軸と範囲の位置関係
の2点を確認しましょう!
その前提として、具体的な問題で練習しましょう!
軸が動く2次関数の最大値・最小値の問題
軸が動く2次関数
👉 軸と範囲の位置関係で場合分け

「場合分け」と聞くと難しく感じるけど、完全パターンだよ!
パターンを覚えてあとは機械的に当てはめればOK!!
☆下に凸の2次関数の最小値について
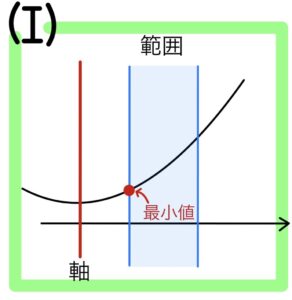
(Ⅰ) 軸 ≦ (範囲の左) のとき
\(x=\)(範囲の左)で最小値をとる
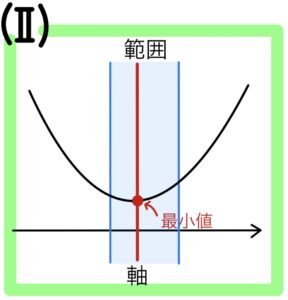
(Ⅱ) (範囲の左) ≦ 軸 ≦ (範囲の右) のとき
\(x=\) 軸で最小値をとる

(Ⅲ) (範囲の右) ≦ 軸 のとき
\(x=\)(範囲の右)で最小値をとる
練習問題
\(a\) は定数とする.
関数\(y=x^2-2ax+a^2+1\) \((0≦x≦2)\) の最小値を求めよ.
【解答】
\(y=x^2-2ax+a^2+1\)を平方完成すると
\(y=(x-a)^2+1\)より
軸は\(x=a\)
軸は\(x=a\),(範囲の左)=0,(範囲の右)=2 を上のパターンに当てはめると
(Ⅰ) \(a≦0\) のとき
\(x=0\) で
最小値:\( a^2+1\)
👆 \(y=x^2-2ax+a^2+1\) に代入
(Ⅱ) \(0≦a≦2\) のとき
\(x=a\) で
最小値:1
(Ⅲ) \(2≦a\) のとき
\(x=2\) で
最小値:\(a^2-4a+5\)
☆下に凸の2次関数の「最大値」について
下に凸の最大値
👉範囲の真中に注目!
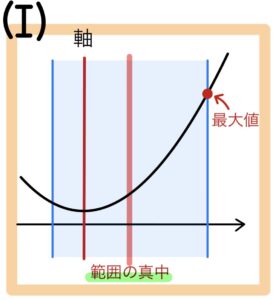
(Ⅰ) 軸 < (範囲の真中) のとき
\(x=\)(範囲の右)で最大値をとる
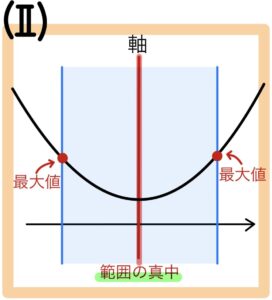
(Ⅱ) 軸 = (範囲の真中) のとき
\(x= \)(範囲の左),(範囲の右)で最大値をとる
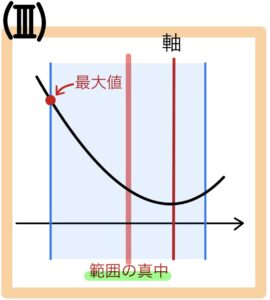
(Ⅲ) (範囲の真中) < 軸 のとき
\(x=\)(範囲の左)で最大値をとる
練習問題
\(a\) は定数とする.
関数\(y=x^2-2ax+a^2+1\) \((0≦x≦2)\) の最大値を求めよ.
【解答】
\(y=x^2-2ax+a^2+1\) を平方完成すると
\(y=(x-a)^2+1\) より
軸は\(x=a\)
軸は\(x=a\),(範囲の真中)=1 を上のパターンに当てはめると
(Ⅰ) \(a<1\) のとき
\(x=2\) で
最大値:\(a^2-4a+5\)
(Ⅱ) \(a=1\) のとき
\(x=0 , 2 \) で
最大値:2
※\(x=0 \) を代入すると\( a^2+1\),
\(x=2 \) を代入すると\(y=a^2-4a+5\)
一見異なるように見えるが,\(a=1\) のときと言う具体的な \(a\) の値が分かっているため、代入するとともに 2 になることが分かる.
(Ⅲ) \(1<a\) のとき
\(x=0\)で
最大値:\( a^2+1\)
範囲の両端が動く2次関数の最大値・最小値の問題
例題(最小値)
\(a\) は定数とする.
関数\(y=x^2-2x\) \((a≦x≦a+2)\) の最小値を求めよ.
【解答】
\(y=x^2-2x\)を平方完成すると
\(y=(x-1)^2-1\)より
軸は\(x=1\)
軸は\(x=1\),(範囲の左)=\(a\),(範囲の右)=\(a+2\) を順に当てはめると

(Ⅰ) \(1≦a\) のとき
\(x=a\) で最小値:\( a^2-2a\)
 (Ⅱ) \(a ≦ 1 ≦ a+2\) のとき
(Ⅱ) \(a ≦ 1 ≦ a+2\) のとき
つまり \(-1 ≦ a ≦ 1\) のとき
\(x=1\) で最小値:-1
 (Ⅲ) \(a+2≦1\) のとき
(Ⅲ) \(a+2≦1\) のとき
つまり \(a ≦-1\) のとき
\(x=a+2\) で最小値:\(a^2+2a\)
例題(最大値)
\(a\) は定数とする.
関数\(y=x^2-2x\) \((a≦x≦a+2)\) の最大値を求めよ.
【解答】
\(y=x^2-2x\)を平方完成すると
\(y=(x-1)^2-1\)より
軸は\(x=1\)
軸は\(x=1\),(範囲の真中)=\(a+1\) を順に当てはめると
 (Ⅰ) \(1<a+1\) のとき
(Ⅰ) \(1<a+1\) のとき
つまり \(0<a\) のとき
\(x=a+2\) で最大値:\(a^2+2a\)
 (Ⅱ) \(1=a+1\) のとき
(Ⅱ) \(1=a+1\) のとき
つまり \(a=0\) のとき
\(x=a , a+2 \)
つまり \(x= 0 , 2 \) で最大値:0
 (Ⅲ) \(a+1<1\) のとき
(Ⅲ) \(a+1<1\) のとき
つまり \(a<0\) のとき
\(x=a\) で最大値:\( a^2-2a\)
2次関数の最大値・最小値の場合分けの問題は、定期考査から大学受験まで頻出テーマです.
しっかりとパターン化し、早く・正確に処理できるように練習を!






コメント