【2021数学ⅠA(第1日程)】第3問(場合の数と確率)
(1)問題と解答・解説《ア〜シ》

解答・解説《ア〜シ》
( ⅰ ) 箱 \(A\) で当たりを引く確率は \(\displaystyle\frac{1}{2}\) ,
ハズレを引く確率は \(1-\displaystyle\frac{1}{2}=\displaystyle\frac{1}{2}\) より
\(3\) 回中ちょうど \(1\) 回当たりを引く確率は
\(_{3}C_{1}\left(\displaystyle\frac{1}{2}\right)\left(\displaystyle\frac{1}{2}\right)^2=\)\(\displaystyle\frac{3}{8}\) ・・・①《アイ》
箱 \(B\) で当たりを引く確率は \(\displaystyle\frac{1}{3}\) ,
ハズレを引く確率は \(1-\displaystyle\frac{1}{3}=\displaystyle\frac{2}{3}\) より
\(3\) 回中ちょうど \(1\) 回当たりを引く確率は
\(_{3}C_{1}\left(\displaystyle\frac{1}{3}\right)\left(\displaystyle\frac{2}{3}\right)^2=\)\(\displaystyle\frac{4}{9}\) ・・・②《ウエ》
( ⅱ ) \(A\) を選ぶ確率と \(B\) を選ぶ確率はともに \(\displaystyle\frac{1}{2}\) であるから,①,②より
\(P(A\cap W)=\displaystyle\frac{1}{2}\times \displaystyle\frac{3}{8}=\displaystyle\frac{3}{16}\) ・・・③
\(P(B\cap W)=\displaystyle\frac{1}{2}\times \displaystyle\frac{4}{9}=\displaystyle\frac{2}{9}\) ・・・④
よって,\(P(W)=P(A\cap W)+P(B\cap W)=\displaystyle\frac{3}{16}+\displaystyle\frac{2}{9}=\displaystyle\frac{59}{144}\) ・・・⑤
であるから,③と⑤より
\(P_{W}(A)=\displaystyle\frac{P(A\cap W)}{P(W)}=\displaystyle\frac{3}{16}\times \displaystyle\frac{144}{59}=\)\(\displaystyle\frac{27}{59}\) ・・・《オ〜ク》
また,④と⑤より
\(P_{W}(B)=\displaystyle\frac{P(B\cap W)}{P(W)}=\displaystyle\frac{2}{9}\times \displaystyle\frac{144}{59}=\)\(\displaystyle\frac{32}{59}\) ・・・《ケ〜シ》

\(P_{W}(B)\) については余事象を利用して,
\(P_{W}(B)=1-P_{W}(A)=1-\displaystyle\frac{27}{59}=\displaystyle\frac{32}{59}\)
と求めてもいいですね!
(2)問題と解答・解説《ス》
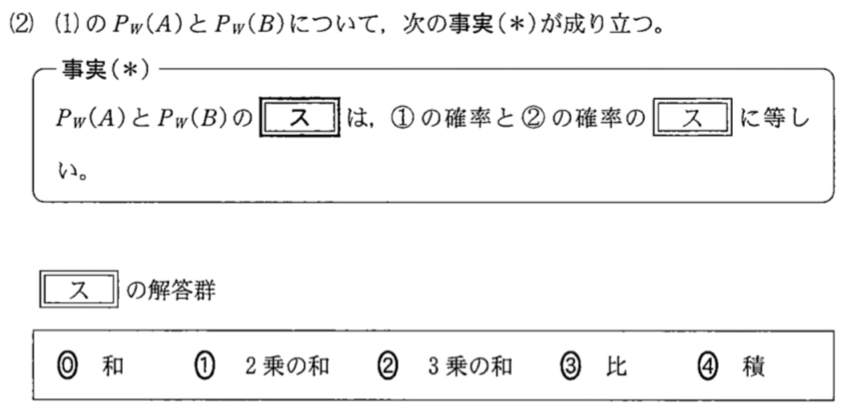
解答・解説《ス》
\(P_{W}(A) : P_{W}(B)=\displaystyle\frac{P(A\cap W)}{P(W)} : \displaystyle\frac{P(B\cap W)}{P(W)}=P(A\cap W) : P(B\cap W)=① : ②\) であるから,《ス:③》
(3)問題と解答・解説《セ〜テ》

解答・解説《セ〜テ》
箱 \(C\) において,\(3\) 回中ちょうど \(1\) 回当たる確率は
\(_{3}C_{1}\left(\displaystyle\frac{1}{4}\right)\left(\displaystyle\frac{3}{4}\right)^2=\displaystyle\frac{27}{64}\) ・・・⑥ であるから,
①,②,⑥より
\(P(W)=P(A\cap W)+P(B\cap W)+P(C\cap W)\)
\(=\displaystyle\frac{1}{3}\times \displaystyle\frac{3}{8}+\displaystyle\frac{1}{3}\times \displaystyle\frac{4}{9}+\displaystyle\frac{1}{3}\times \displaystyle\frac{27}{64}\)
\(=\displaystyle\frac{1}{3}\times \left(\displaystyle\frac{3}{8}+\displaystyle\frac{4}{9}+\displaystyle\frac{27}{64}\right)=\displaystyle\frac{715}{3\times 9\times 64}\) ・・・⑦
したがって①と⑦より
\(P_{W}(A)=\displaystyle\frac{P(A\cap W)}{P(W)}=\left(\displaystyle\frac{1}{3}\times \displaystyle\frac{3}{8}\right)\times \displaystyle\frac{3\times 9\times 64}{715}=\)\(\displaystyle\frac{216}{715}\) ・・・《セ〜テ》
(4)問題と解答・解説《ト》

解答・解説《ト》
箱 \(D\) において,\(3\) 回中ちょうど \(1\) 回当たる確率は
\(_{3}C_{1}\left(\displaystyle\frac{1}{5}\right)\left(\displaystyle\frac{4}{5}\right)^2=\displaystyle\frac{48}{125}\) ・・・⑧ であり,花子さんの考え(《ス》について) を用いると
\(P_{W}(A) : P_{W}(B) : P_{W}(C) : P_{W}(D) = \displaystyle\frac{3}{8} : \displaystyle\frac{4}{9} : \displaystyle\frac{27}{64} : \displaystyle\frac{48}{125}\\=0.375 : 0.444\cdots : 0.421\cdots : 0.384\)
であるから,可能性が高い方から順に並べると ⑧ \(B , C , D , A\) ・・・《ト》









コメント