2次関数の問題において、絶対におさえておきたい頻出テーマが2つあります。
1つは「最大値・最小値の場合分け」の問題!
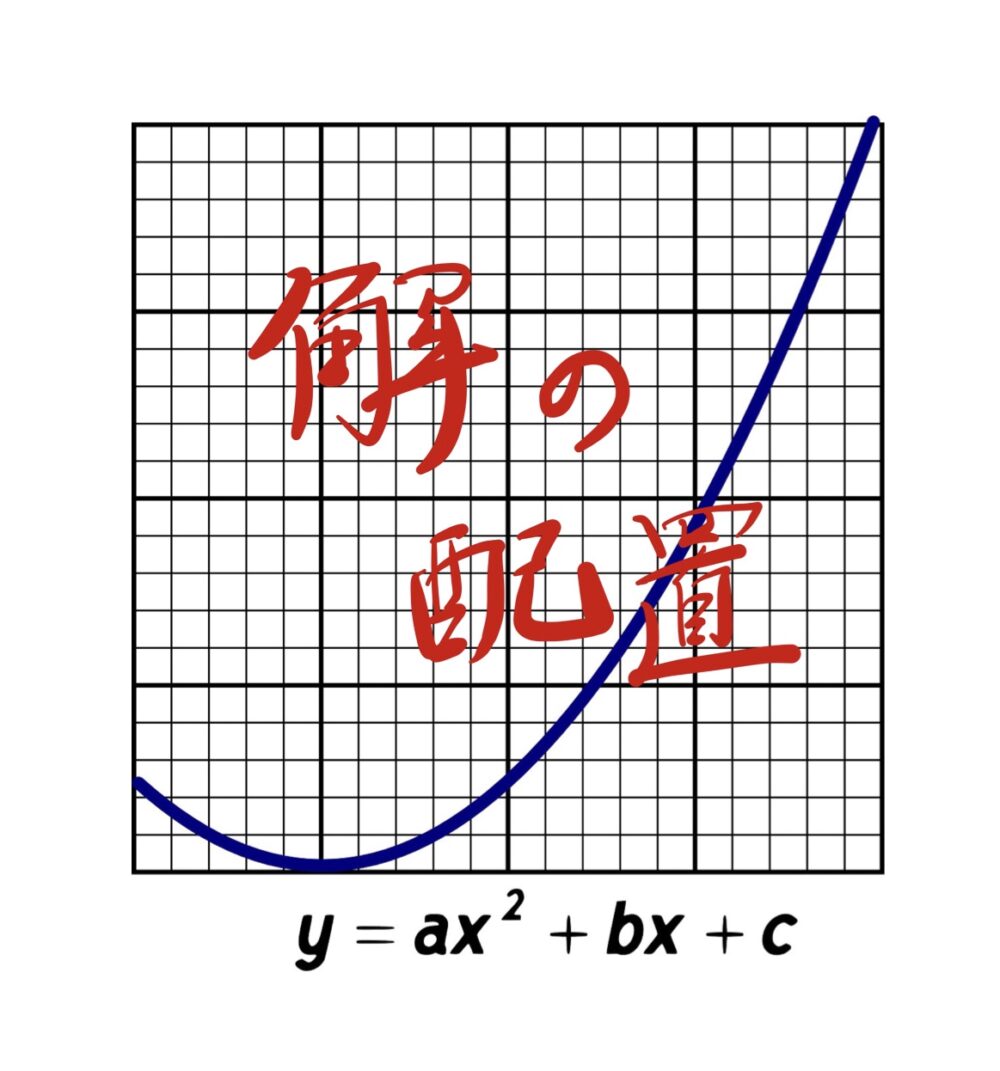
そしてもう1つが「解の配置(分離)」の問題!
この問題もまた完全パターンものになりますので、しっかりとパターンをおさえましょう!
まず初めに、解の配置の問題がどのような問題なのか?
・2次方程式が実数解を持つ
☞ 判別式Dを考える
・2次方程式が○○の範囲に実数解を持つ
☞解の配置(分離)の問題
ただ実数解を持つだけでなく、ある範囲に解を持つという問題です
解の配置(分離)の有名2パターン
解の配置の問題は、大きく分けると2パターンあります。
それぞれのパターンを確認しましょう!
αより大きい(小さい)異なる2つの実数解をもつ
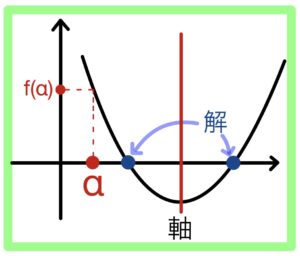 ☞条件3種類について考える
☞条件3種類について考える
① 判別式\(D\)
② 軸とα大小
③ \(f(α)\)の符号
αより大きい解と小さい解をそれぞれ持つ
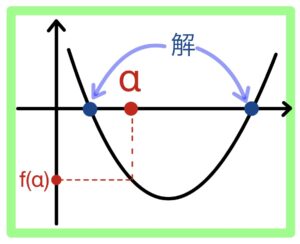 ☞条件1種類について考える
☞条件1種類について考える
① \(f(α)\)の符号
練習問題 パターン①
【例題】
2次関数 \(y=x^2-(a+3)x+a^2\) のグラフが \(x\) 軸の \(x>1\) の部分と異なる2点で交わるとき、定数 \(a\) の値の範囲を求めよ.
【考え方】
2つのグラフ (\(y=x^2-(a+3)x+a^2\) と \(x\) 軸(\(y=0\))) の交点の個数
☞ 方程式 \(x^2-(a+3)x+a^2=0\) の解の個数
☞ \(x>1\) の範囲で、方程式 \(x^2-(a+3)x+a^2=0\) が異なる2つの解を持つための条件
☞解の配置のパターンの1つ目
【解答】
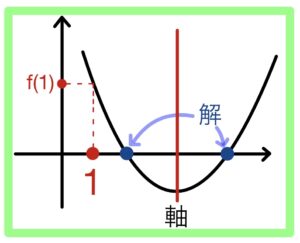
① 判別式 \(D>0\)
\(D={-(a+3)}^2-4 \cdot 1 \cdot a^2\)
\(=-3(a+1)(a-3)>0\)
よって \(-1<a<3\)
② \(軸>1\)
軸は、\(x=\displaystyle\frac{a+3}{2}\)より
\(\displaystyle\frac{a+3}{2}>1\)
よって \(a>-1 \)
③ \(f(1)>0\)
\(f(1)=1-(a+3)+a^2=(a+1)(a-2)>0\)
よって \(a<-1 , 2<a \)
①~③の共通範囲を求めて、\(2<a<3\)
練習問題 パターン②
【例題】
2次関数 \(y=x^2-(a+3)x+a^2\) のグラフが \(x\) 軸の \(x>1\) の部分と \(x<1\) の部分でそれぞれ交わるとき、定数 \(a\) の値の範囲を求めよ.
【考え方】
2つのグラフ (\(y=x^2-(a+3)x+a^2\) と \(x\) 軸(\(y=0\)))の交点の個数
☞方程式 \(x^2-(a+3)x+a^2=0\) の解の個数
☞ \(x>1\) と \(x<1\) の範囲で、方程式 \(x^2-(a+3)x+a^2=0\) がそれぞれ解を持つための条件
☞ 解の配置のパターンの2つ目
【解答】
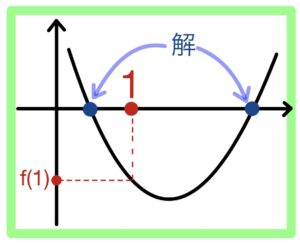 ① \(f(1)<0\)
① \(f(1)<0\)
\(f(1)=1-(a+3)+a^2=(a+1)(a-2)<0\)
よって \(-1<a<2 \)
条件式を立てる練習
【練習】2次関数 \(y=x^2-mx\) のグラフについて
(1) \(x\) 軸の負の部分と、異なる2点で交わる
(2) \(x\) 軸の正の部分と負の部分で交わる
(3) \(x\) 軸の \(1≦x≦3\) の部分と、異なる2点で交わる
※条件式を立てるだけで、計算は省略します。
(1)はパターンの1つ目
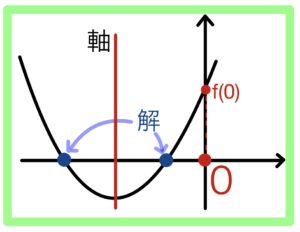 ① \(D>0\)
① \(D>0\)
② 軸<0
③ \(f(0)>0\)
(2)はパターンの2つ目
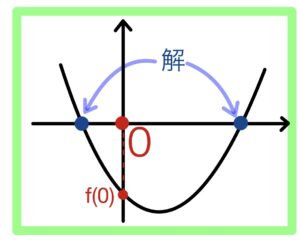 ① \(f(0)<0\)
① \(f(0)<0\)
(3)はパターンの1つ目
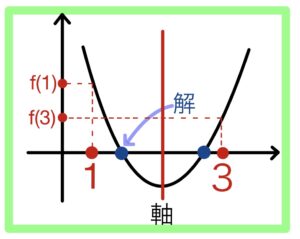 ① \(D>0\)
① \(D>0\)
② \(1<軸<3\)
③ \(f(1)≧0\) , \(f(3)≧0\)
※③については、基準となる α が2つ(-1と3) あったため、それぞれの \(f(α)\) の符号を考えた.
まとめ
- ある範囲で解を持つ👉解の分離
- 図を書く→ 条件式 → 計算 の3STEPで処理!






コメント